熱伝導方程式の初期値問題を解く
熱伝導方程式を指定する.
In[1]:=
heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];方程式の初期条件を与える.
In[2]:=
ic = u[x, 0] == E^(-x^2);初期値問題を解く.
In[3]:=
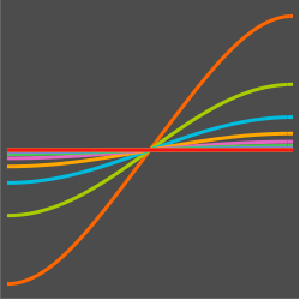
sol = DSolveValue[{heqn, ic }, u[x, t], {x, t}]Out[3]=
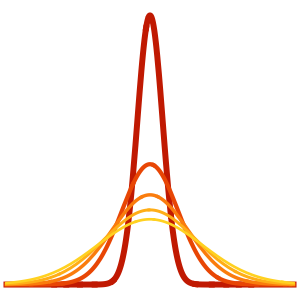
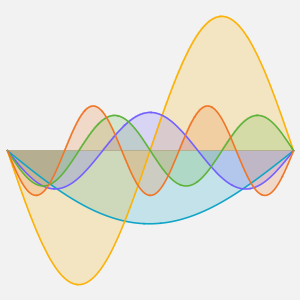
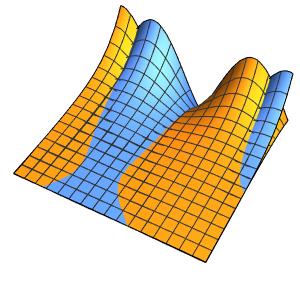
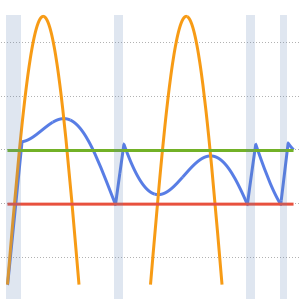
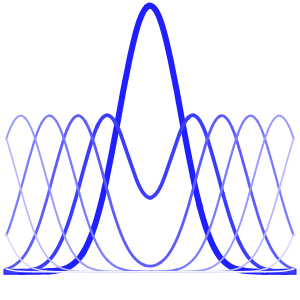
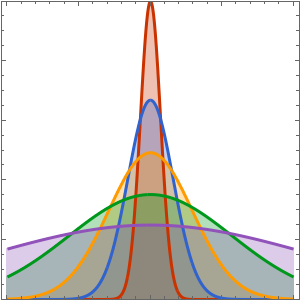
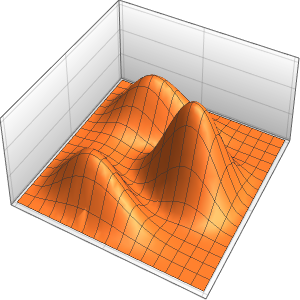
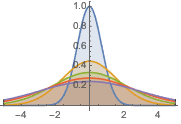
時間の経過にともなう熱の拡散を可視化する.
In[4]:=
Plot[Evaluate[Table[sol, {t, 0, 4}]], {x, -5, 5}, PlotRange -> All,
Filling -> Axis]Out[4]=
区分的初期データを持つ熱伝導方程式の初期値問題.
In[5]:=
ic = u[x, 0] == UnitBox[x];In[6]:=
sol = DSolveValue[{heqn, ic }, u[x, t], {x, t}]Out[6]=
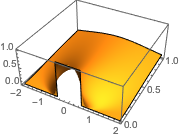
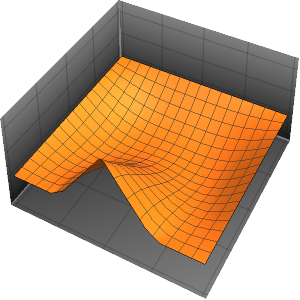
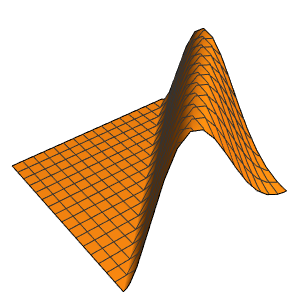
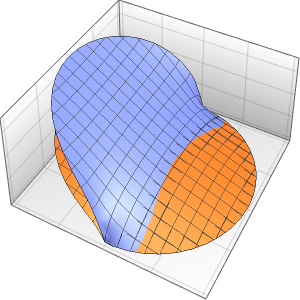
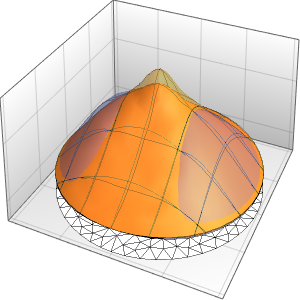
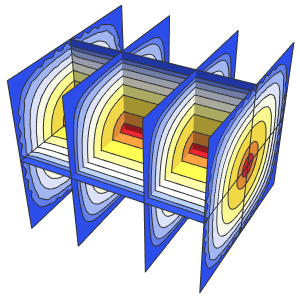
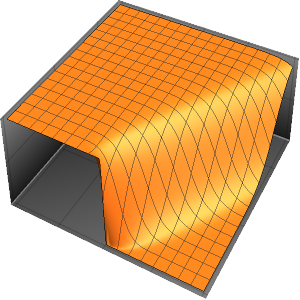
初期データにおける不連続性はすぐに滑らかにされる.
In[7]:=
Plot3D[sol, {x, -2, 2}, {t, 0, 1}, PlotRange -> All,
PlotPoints -> 250, Mesh -> None]Out[7]=