求解热传导方程的初值问题
指定热传导方程.
In[1]:=
heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];规定方程的初始条件.
In[2]:=
ic = u[x, 0] == E^(-x^2);求解初值问题.
In[3]:=
sol = DSolveValue[{heqn, ic }, u[x, t], {x, t}]Out[3]=
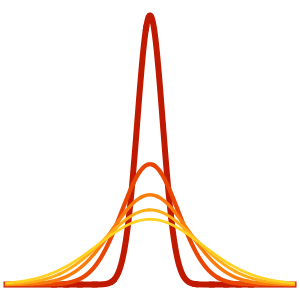
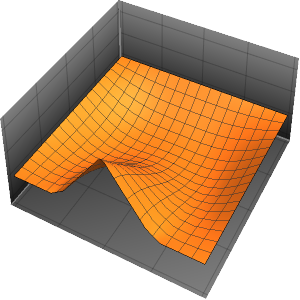
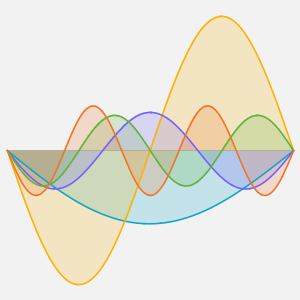
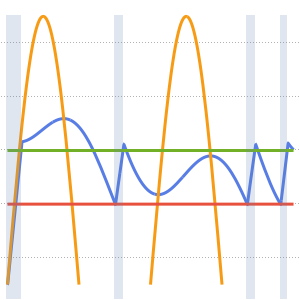
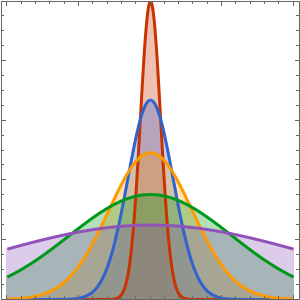
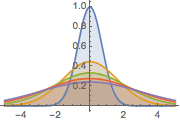
可视化热量随时间的扩散.
In[4]:=
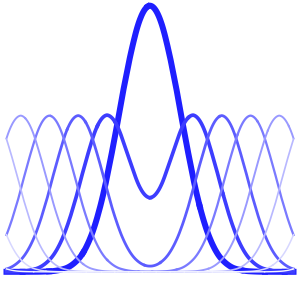
Plot[Evaluate[Table[sol, {t, 0, 4}]], {x, -5, 5}, PlotRange -> All,
Filling -> Axis]Out[4]=
用分段初始数据求解热传导方程的初值问题.
In[5]:=
ic = u[x, 0] == UnitBox[x];In[6]:=
sol = DSolveValue[{heqn, ic }, u[x, t], {x, t}]Out[6]=
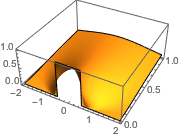
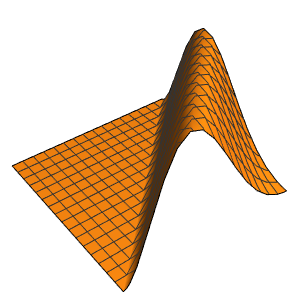
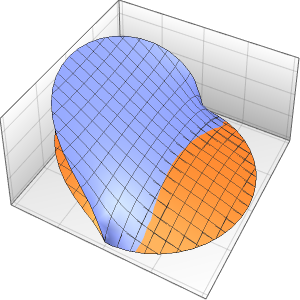
初始数据中的不连续处立即被平滑化.
In[7]:=
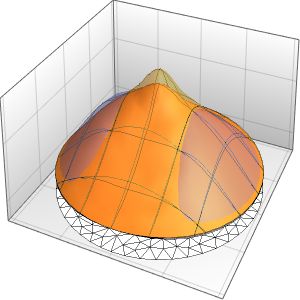
Plot3D[sol, {x, -2, 2}, {t, 0, 1}, PlotRange -> All,
PlotPoints -> 250, Mesh -> None]Out[7]=