研究激波的形成
使用黏性流动的伯格斯方程(Burgers' equation)研究激波的形成.
In[1]:=
TraditionalForm[BurgersEquation = \!\(
\*SubscriptBox[\(\[PartialD]\), \({t}\)]\(u[x, t]\)\) + u[x, t] \!\(
\*SubscriptBox[\(\[PartialD]\), \({x}\)]\(u[x,
t]\)\) == \[Epsilon] \!\(
\*SubscriptBox[\(\[PartialD]\), \({x, 2}\)]\(u[x, t]\)\)]Out[1]//TraditionalForm=
规定一个分段初始条件.
In[2]:=
InitialCondition = u[x, 0] == Piecewise[{{1, x < 0}}]; 求解初始值问题.
In[3]:=
dsol = DSolveValue[{BurgersEquation, InitialCondition},
u[x, t], {x, t}]Out[3]=
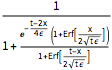
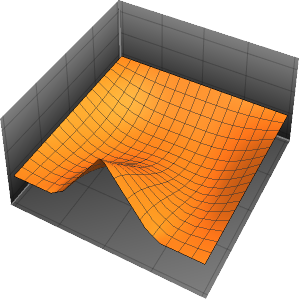
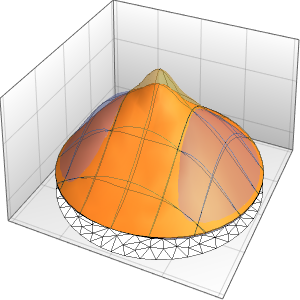
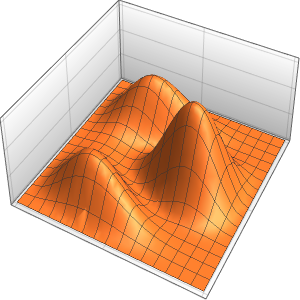
对于任何正值 ϵ,方程的解都是光滑的.
In[4]:=
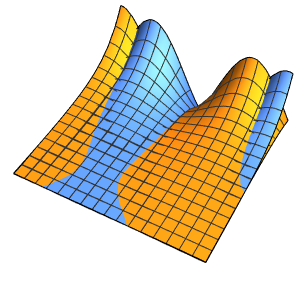
Plot3D[dsol /. {\[Epsilon] -> 1/10}, {x, -2, 2}, {t, 0.001, 5}]Out[4]=
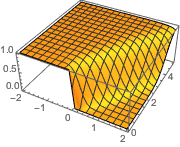
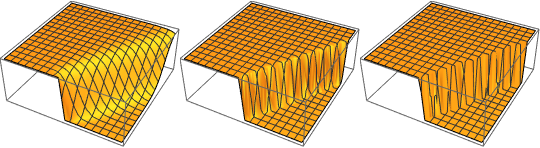
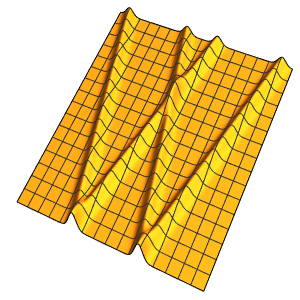
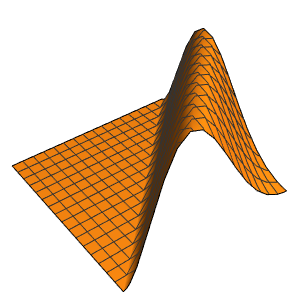
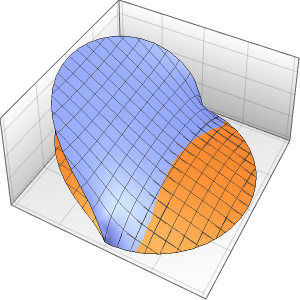
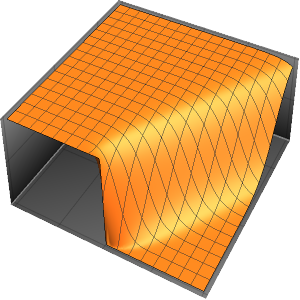
在 ϵ 趋近于 0 的极限点,方程的解会出现一个激波形式的不连续.
In[5]:=

Row[Table[Plot3D[dsol, {x, -2, 2}, {t, 0.001, 5},
Exclusions -> None, Ticks -> None],
{\[Epsilon], {1/10, 1/100, 1/1000}}]]Out[5]=