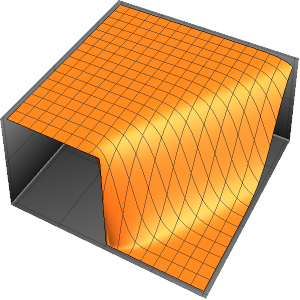
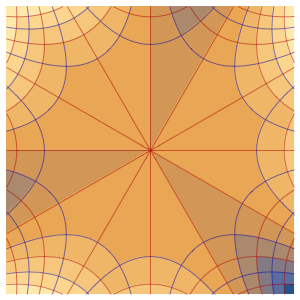
Étudiez la formation d'une onde de choc
Utilisez l'équation de Burgers pour l'écoulement d'un fluide visqueux afin d'étudier la formation d'une onde de choc.
In[1]:=
TraditionalForm[BurgersEquation = \!\(
\*SubscriptBox[\(\[PartialD]\), \({t}\)]\(u[x, t]\)\) + u[x, t] \!\(
\*SubscriptBox[\(\[PartialD]\), \({x}\)]\(u[x,
t]\)\) == \[Epsilon] \!\(
\*SubscriptBox[\(\[PartialD]\), \({x, 2}\)]\(u[x, t]\)\)]Out[1]//TraditionalForm=
Établissez une condition initiale par morceaux.
In[2]:=
InitialCondition = u[x, 0] == Piecewise[{{1, x < 0}}]; Résolvez le problème de la valeur initiale.
In[3]:=
dsol = DSolveValue[{BurgersEquation, InitialCondition},
u[x, t], {x, t}]Out[3]=
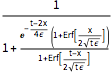
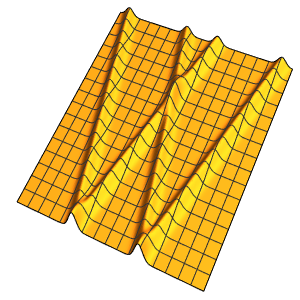
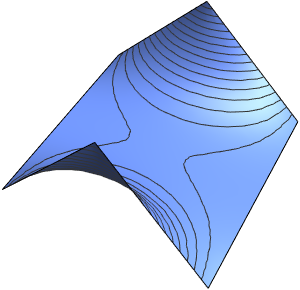
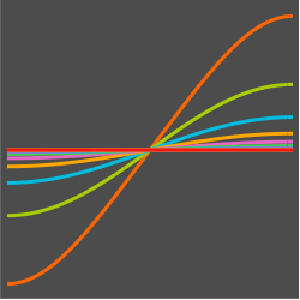
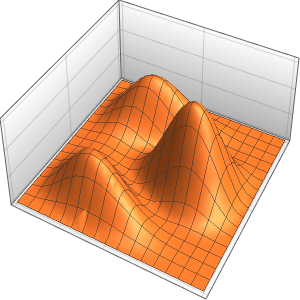
La solution est lisse pour toute valeur positive de ϵ.
In[4]:=
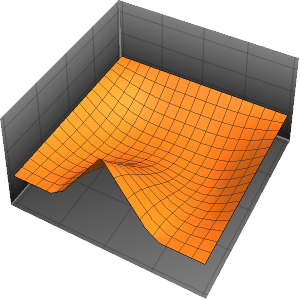
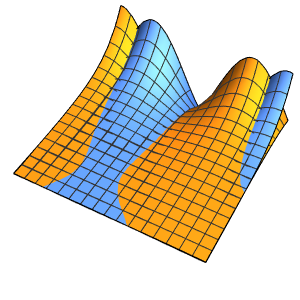
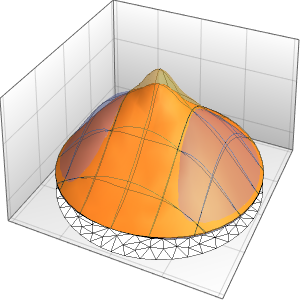
Plot3D[dsol /. {\[Epsilon] -> 1/10}, {x, -2, 2}, {t, 0.001, 5}]Out[4]=
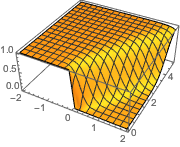
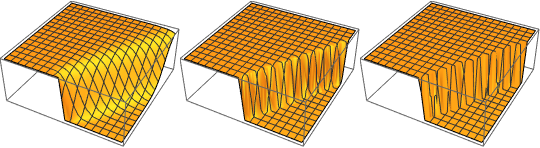
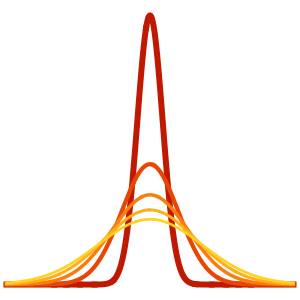
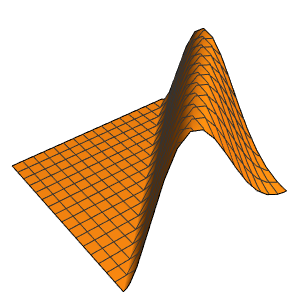
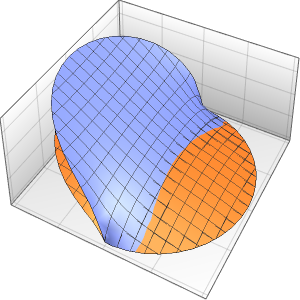
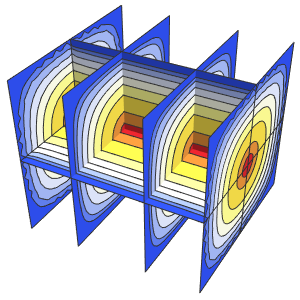
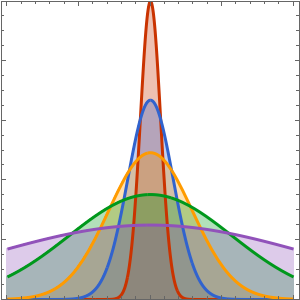
La solution développe une discontinuité de choc dans la limite quand ϵ s'approche de 0.
In[5]:=

Row[Table[Plot3D[dsol, {x, -2, 2}, {t, 0.001, 5},
Exclusions -> None, Ticks -> None],
{\[Epsilon], {1/10, 1/100, 1/1000}}]]Out[5]=