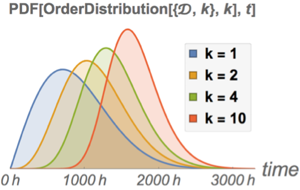
数量母数の分布
平均70インチ,標準偏差6.5インチの正規分布で身長の分布の近似を行う.分布は,Quantityを対応する平均と標準偏差の母数として使って構築することができ,適切なQuantityDistributionを返す.
In[1]:=
height\[ScriptCapitalD] =
NormalDistribution[Quantity[70, "Inches"], Quantity[6.5, "Inches"]]Out[1]=
分布は,指定の単位で確率変数を表す.
In[2]:=
averageHeight = Mean[height\[ScriptCapitalD]]Out[2]=
適切な数量引数を使って分布の計算を行う.
In[3]:=
CDF[height\[ScriptCapitalD], Quantity[170, "Centimeters"]]Out[3]=
ある人の身長が65インチから72インチの間である確率を計算する.
In[4]:=
Probability[Quantity[65, "in"] < x < Quantity[72, "in"],
x \[Distributed] height\[ScriptCapitalD]]Out[4]=
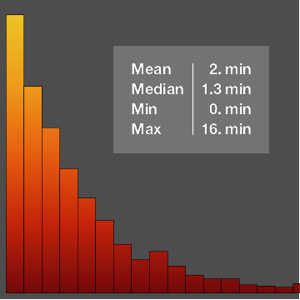
この身長の分布を仮定して,帽子が人の頭から地面に落ちるまでの平均時間を求める.
In[5]:=

NExpectation[Sqrt[(2 h)/Entity["Planet", "Earth"]["Gravity"]],
h \[Distributed] height\[ScriptCapitalD]]Out[5]=