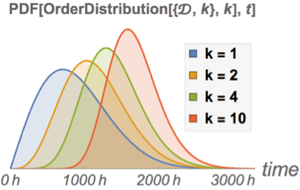
Loi avec des paramètres de grandeurs

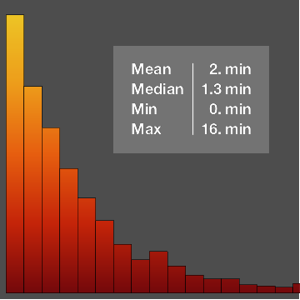
Approximez la répartition de la taille par une loi normale dont la moyenne est de 70 pouces (177,8 cm) et l'écart type de 6,5 pouces (16,5 cm). La loi peut être construite à l'aide de Quantity en tant que paramètres de moyenne et d'écart-type correspondant et donnera une QuantityDistribution appropriée.

In[1]:=

height\[ScriptCapitalD] = NormalDistribution[Quantity[70, "Inches"], Quantity[6.5, "Inches"]]

Out[1]=

La loi représente une variable aléatoire dans les unités spécifiées.

In[2]:=

averageHeight = Mean[height\[ScriptCapitalD]]

Out[2]=

Calculez avec la loi en utilisant des arguments quantitatifs appropriés.

In[3]:=

CDF[height\[ScriptCapitalD], Quantity[170, "Centimeters"]]

Out[3]=

Calculez la probabilité que la hauteur d'une personne soit entre 65 et 72 pouces (165 et 182,9 cm).

In[4]:=

Probability[Quantity[65, "in"] < x < Quantity[72, "in"], x \[Distributed] height\[ScriptCapitalD]]

Out[4]=

En supposant cette loi de hauteur, trouvez le temps moyen d'un chapeau tombant de la tête d'une personne sur Terre.

In[5]:=

NExpectation[Sqrt[(2 h)/Entity["Planet", "Earth"]["Gravity"]], h \[Distributed] height\[ScriptCapitalD]]

Out[5]=