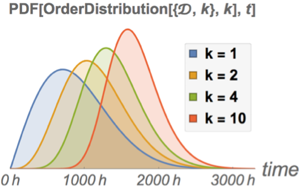
含有数量参数的分布
用均值为 70 英寸、标准差为 6.5 英寸的标准分布近似身高的分布. 可以用 Quantity 作为相应的均值和标准差参数来构建分布,产生合适的 QuantityDistribution.
In[1]:=
height\[ScriptCapitalD] =
NormalDistribution[Quantity[70, "Inches"], Quantity[6.5, "Inches"]]Out[1]=
分布表示了带有指定单位的随机变量.
In[2]:=
averageHeight = Mean[height\[ScriptCapitalD]]Out[2]=
利用适当的数量参数对分布进行计算.
In[3]:=
CDF[height\[ScriptCapitalD], Quantity[170, "Centimeters"]]Out[3]=
计算人的身高在65和72英寸之间的概率.
In[4]:=
Probability[Quantity[65, "in"] < x < Quantity[72, "in"],
x \[Distributed] height\[ScriptCapitalD]]Out[4]=
在这样的身高分布的情况下,计算一顶帽子从人的头部落到地上所花费的平均时间.
In[5]:=

NExpectation[Sqrt[(2 h)/Entity["Planet", "Earth"]["Gravity"]],
h \[Distributed] height\[ScriptCapitalD]]Out[5]=