Wolfram Language™

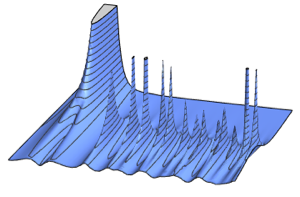
Separações de valore próprios de distribuições de Gauss

As separações de valores próprios (diferenças de valores próprios consecutivos) de distribuições de matriz têm uma forma limite universal que é observada em muitos sistemas na natureza, como as separações de átomos pesados a nível de energia.

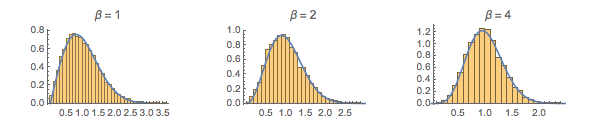
Faça uma amostra de separações de valores próprios de matrizes 2×2 de diferentes conjuntos de Gauss.

In[1]:=

gaussiandists = {GaussianOrthogonalMatrixDistribution[2], GaussianUnitaryMatrixDistribution[2], GaussianSymplecticMatrixDistribution[2]};

In[2]:=

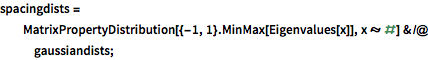
spacingdists = MatrixPropertyDistribution[{-1, 1}.MinMax[Eigenvalues[x]], x \[Distributed] #] & /@ gaussiandists;

In[3]:=

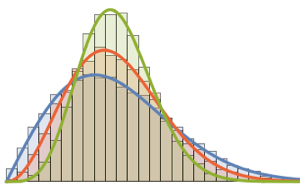
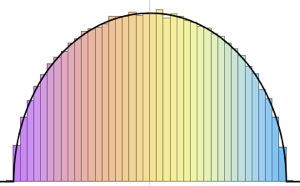
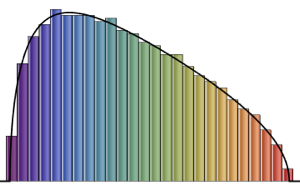
gaps = Normalize[RandomVariate[#, 10000], Mean] & /@ spacingdists;

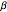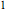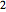Compare os histogramas de cada distribuição com sua forma fechada, também conhecida como suposição de Wigner para os índices de Dyson de , , e .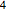

In[4]:=

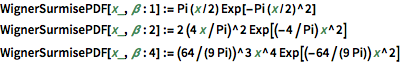
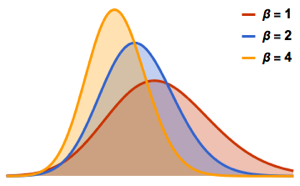
WignerSurmisePDF[x_, \[Beta] : 1] := Pi (x/2) Exp[-Pi (x/2)^2] WignerSurmisePDF[x_, \[Beta] : 2] := 2 (4 x/Pi)^2 Exp[(-4/Pi) x^2] WignerSurmisePDF[ x_, \[Beta] : 4] := (64/(9 Pi))^3 x^4 Exp[(-64/(9 Pi)) x^2]

In[5]:=

histogram = Histogram[#, {0.1}, PDF] & /@ gaps; plot = Plot[WignerSurmisePDF[x, #] , {x, 0, 3}] & /@ {1, 2, 4}; GraphicsRow@ MapThread[ Show[#1, #2, ImageSize -> 180, PlotLabel -> Row[{"\[Beta] = ", #3}]] &, {histogram, plot, {1, 2, 4}}]

Out[5]=