Conjuntos de Gauss (GOE, GUE, ...)
Os conjuntos de Gauss são famílias de matrizes aleatórias normalmente distribuídas com distribuições invariantes sob diferentes transformações unitárias. Elas são bem estudadas, em parte devido à tratabilidade analítica, mas também devido aos espectros associados que se aproximam bastante a muitos sistemas com grandes graus de liberdade. Exemplos destes sistemas são encontrados na física, finanças, e biologia.
Matrizes de um conjunto ortogonal de Gauss (GOE) são simétricos. »
In[1]:=
goe = RandomVariate[GaussianOrthogonalMatrixDistribution[5]];In[2]:=
SymmetricMatrixQ[goe]Out[2]=
Matrizes de um conjunto unitário de Gauss (GUE) são hermitianas. »
In[3]:=
gue = RandomVariate[GaussianUnitaryMatrixDistribution[5]];In[4]:=
HermitianMatrixQ[gue]Out[4]=
Matrizes de um conjunto simplético de Gauss (GSE) são simplécticas hermitianas. »
mostre o input completo da Wolfram Language
In[6]:=
gse = RandomVariate[GaussianSymplecticMatrixDistribution[5]];In[7]:=
symplecticMatrixQ[gse] && HermitianMatrixQ[gse]Out[7]=
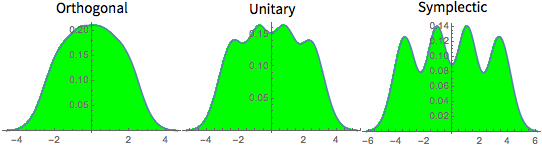
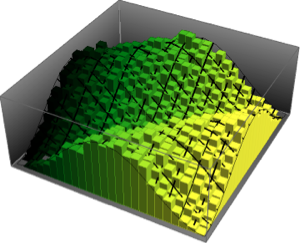
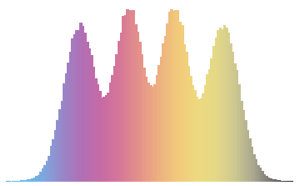
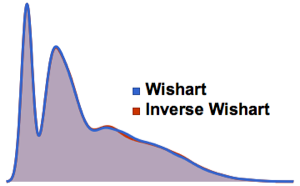
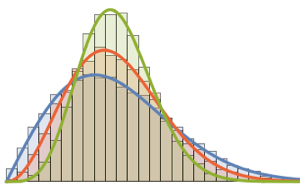
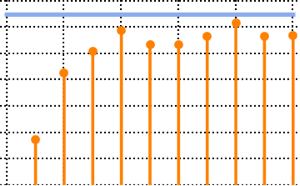
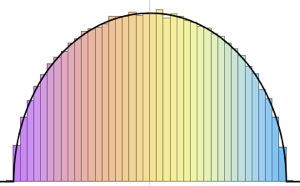
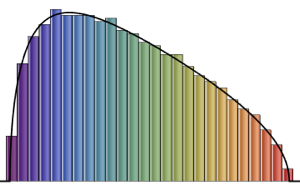
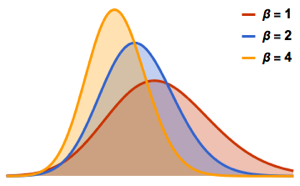
Distribuição de valores próprios para matrizes de conjuntos de Gauss em pequenas dimensões.
mostre o input completo da Wolfram Language
Out[8]=