Propriedades de distribuição de matriz

As estatísticas de menor dimensão derivadas das matrizes aleatórias desempenham papéis importantes na caracterização de conjuntos de matriz. Em várias situações limites, as distribuições destas estatísticas colapsam em diferentes classes de universalidade. MatrixPropertyDistribution fornece um acesso conveniente para fazer amostras e calcular a aproximação numérica dessas propriedades derivadas.

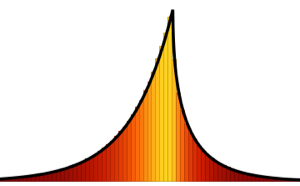
Faça uma amostra dos dois maiores valores próprios de um conjunto unitário de Gauss.

In[1]:=

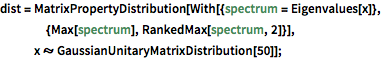
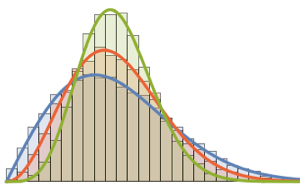
dist = MatrixPropertyDistribution[With[{spectrum = Eigenvalues[x]}, {Max[spectrum], RankedMax[spectrum, 2]}], x \[Distributed] GaussianUnitaryMatrixDistribution[50]];

In[2]:=

RandomVariate[dist]

Out[2]=

Visualize a distribuição conjunta dos maiores valores próprios com base no resultado da amostragem.

In[3]:=

sample = RandomVariate[dist, 10^4];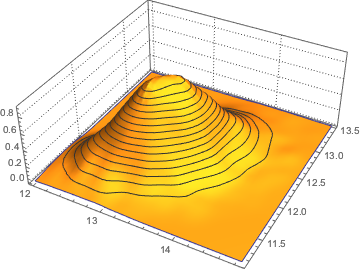

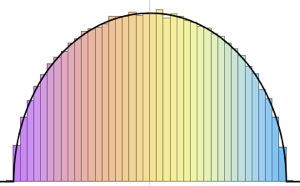
In[4]:=

SmoothHistogram3D[sample, "Scott", "PDF", PlotTheme -> "Detailed", ImageSize -> Medium]

Out[4]=

Faça uma amostra do determinante de matrizes de um conjunto ortogonal de Gauss e compara a distribuição empírica com a expressão de forma fechada.

In[5]:=

dist = MatrixPropertyDistribution[Det[x], x \[Distributed] GaussianOrthogonalMatrixDistribution[2]]; dets = RandomVariate[dist, 10^6];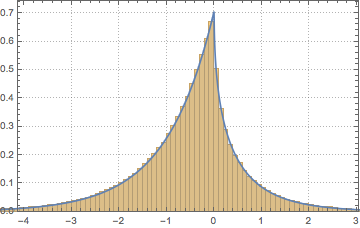

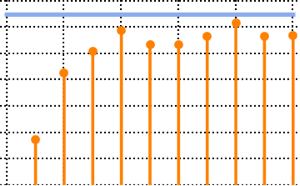
In[6]:=

empirical = Histogram[dets, {0.1}, PDF, PlotTheme -> "Detailed", ImageSize -> Medium]; detpdf[y_] := 1/Sqrt[2] Exp[ y] Piecewise[{{Erfc[Sqrt[2 y]], y >= 0}, {1, y < 0}}]; analytical = Plot[detpdf[y], {y, -5, 4}, Exclusions -> None, PlotLegends -> None, PlotTheme -> "Detailed", ImageSize -> Medium, Filling -> Axis]; Show[empirical, analytical]

Out[6]=

Aproxime a média do determinante através de amostragem pelo método Monte Carlo e compare-o com o valor real.

In[7]:=

{N@Mean[dist], Integrate[x detpdf[x], {x, -Infinity, Infinity}]}

Out[7]=