Wolfram言語™

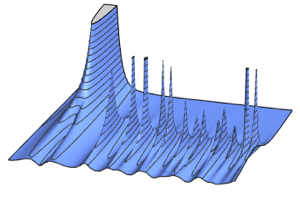
ガウス分布の固有値の間隔

行列分布の固有値の間隔（連続する固有値の差分）は，重原子のエネルギー準位の間隔等，自然の中の多くの系で見ることのできる普遍的な極限形を持つ．

さまざまなガウスアンサンブルから2×2行列の固有値間隔をサンプリングする．

In[1]:=

gaussiandists = {GaussianOrthogonalMatrixDistribution[2], GaussianUnitaryMatrixDistribution[2], GaussianSymplecticMatrixDistribution[2]};

In[2]:=

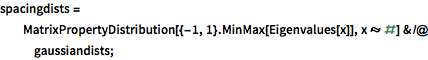
spacingdists = MatrixPropertyDistribution[{-1, 1}.MinMax[Eigenvalues[x]], x \[Distributed] #] & /@ gaussiandists;

In[3]:=

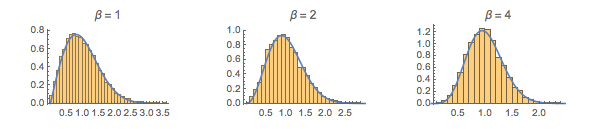
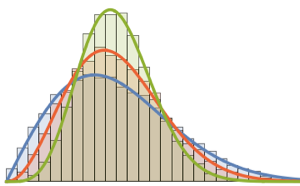
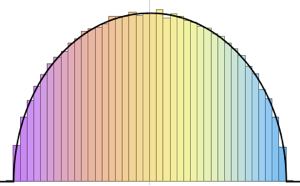
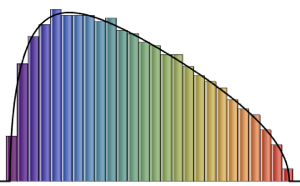
gaps = Normalize[RandomVariate[#, 10000], Mean] & /@ spacingdists;

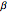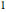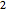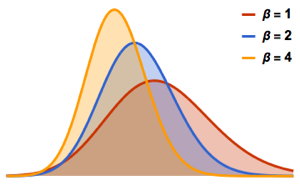
各分布のヒストグラムを，Dyson指数 が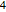，，の場合のWigner推量として知られる，それぞれの閉形式と比較する．

In[4]:=

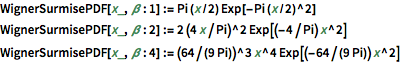
WignerSurmisePDF[x_, \[Beta] : 1] := Pi (x/2) Exp[-Pi (x/2)^2] WignerSurmisePDF[x_, \[Beta] : 2] := 2 (4 x/Pi)^2 Exp[(-4/Pi) x^2] WignerSurmisePDF[ x_, \[Beta] : 4] := (64/(9 Pi))^3 x^4 Exp[(-64/(9 Pi)) x^2]

In[5]:=

histogram = Histogram[#, {0.1}, PDF] & /@ gaps; plot = Plot[WignerSurmisePDF[x, #] , {x, 0, 3}] & /@ {1, 2, 4}; GraphicsRow@ MapThread[ Show[#1, #2, ImageSize -> 180, PlotLabel -> Row[{"\[Beta] = ", #3}]] &, {histogram, plot, {1, 2, 4}}]

Out[5]=