Transformée intégrale d'EntityStore

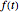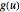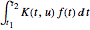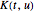Une transformée intégrale est une opération mathématique qui applique une fonction à travers une autre au moyen d'une intégrale de la forme où est connu comme le noyau. Les transformées intégrales sont extrêmement importantes dans de nombreux domaines d'intérêt, notamment le traitement des signaux, l'imagerie médicale et la théorie des probabilités. La construction d'un magasin d'entités contenant les propriétés de transformées importantes est illustrée ici.

Le magasin d'entités peut être codé à la main en enregistrant les propriétés les plus importantes des transformées intégrales dans une structure de données dans EntityStore.

In[1]:=

EntityStore[<| "Types" -> <| "IntegralTransform" -> <| "Entities" -> <| "ExponentialFourierTransform" -> <| "Label" -> "exponential Fourier transform", "StandardName" -> "ExponentialFourierTransform", "StandardNotation" -> Hold[f[t]], "Definition" -> Inactive[FourierTransform][f[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[Integrate][ E^(I t z) f[t], {t, -\[Infinity], \[Infinity]}]/Sqrt[ 2 \[Pi]], "GeneralProperties" -> <| "Linearity" -> {Inactive[FourierTransform][ a f[t] + b g[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) a Inactive[FourierTransform][f[t], t, z] + b Inactive[FourierTransform][g[t], t, z], Inactive[FourierTransform][f[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[-t] UnitStep[t], t, -z] + Inactive[FourierTransform][f[t] UnitStep[t], t, z]}, "Reflection" -> {Inactive[FourierTransform][f[-t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, -z]}, "Dilation" -> {ConditionalExpression[ Inactive[FourierTransform][f[a t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, z/a]/Abs[a], a \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals && a \!\(\* TagBox["!=", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"!="]\) 0]}, "Shifting or translation" -> {ConditionalExpression[ Inactive[FourierTransform][f[-a + t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) E^(I a z) Inactive[FourierTransform][f[t], t, z], a \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals]}|>|>|>|>|>|>]

Out[1]=

Une version plus complète peut être récupérée à partir du CloudObject suivant.

In[2]:=

itstore = CloudGet[CloudObject[ "https://www.wolframcloud.com/objects/c21b356b-607a-406c-af91-\ 5088f435fe99"]]

Out[2]=

Enregistrez le magasin pour cette session.

In[3]:=

PrependTo[$EntityStores, itstore];

Visualisez les entités dans le magasin.

In[4]:=

EntityValue["IntegralTransform", "Entities"]

Out[4]=

Ajoutez une nouvelle transformée.

In[5]:=

Entity["IntegralTransform", "HilbertTransform"]["Label"] = "Hilbert transform"; Entity["IntegralTransform", "HilbertTransform"]["Definition"] = Inactive[HilbertTransform][f[t], t, x] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) 1/\[Pi] Inactive[Integrate][f[t]/( t - x), {t, -\[Infinity], \[Infinity]}, PrincipalValue -> True, Assumptions -> x \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals];

Renvoyez les propriétés actuellement disponibles pour les transformées intégrales.

In[6]:=

EntityValue["IntegralTransform", "Properties"]

Out[6]=

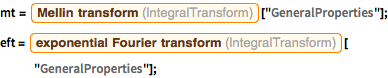
Récupérez les définitions des transformées exponentielles de Fourier et de Mellin.

In[7]:=

EntityValue[ Entity["IntegralTransform", "LaplaceTransform"], "Definition"]

Out[7]=

In[8]:=

EntityValue[ Entity["IntegralTransform", "MellinTransform"], "Definition"]

Out[8]=

Comparez avec les expressions renvoyées par les fonctions intégrées correspondantes.

In[9]:=

Activate[EntityValue[Entity["IntegralTransform", "LaplaceTransform"], "Definition"][[2]] /. f :> Function[t, ArcTan[t]]]

Out[9]=

In[10]:=

LaplaceTransform[ArcTan[t], t, z]

Out[10]=

Affichez la propriété de convolution de la transformée Z.

In[11]:=

Entity["IntegralTransform", "ZTransform"][ "GeneralProperties"]["Convolution"]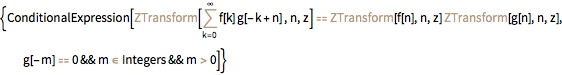

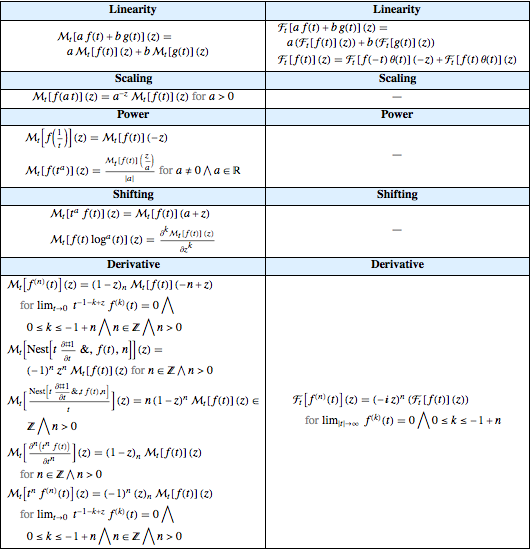
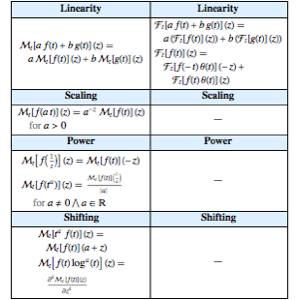
Out[11]=

Comparez les propriétés actuellement stockées des transformées exponentielles de Fourier et de Mellin.

In[12]:=

format[l_] := If[MatchQ[l, _Missing], "\[LongDash]", Activate[HoldForm @@ ({Column[l]} /. HoldPattern[ConditionalExpression[a_, b_]] :> Row[{a, Style[ " for ", Gray], b}])]]

In[13]:=

mt = Entity["IntegralTransform", "MellinTransform"][ "GeneralProperties"]; eft = Entity["IntegralTransform", "ExponentialFourierTransform"][ "GeneralProperties"];

In[14]:=

Grid[Take[ Flatten[{{Style[#, Bold], Style[#, Bold]}, {format@mt[#], format@eft[#]}} & /@ DeleteDuplicates[Join[Keys[mt], Keys[eft]]], 1], 10], Dividers -> All, Background -> {None, {{LightBlue, White}}}] // TraditionalForm

Out[14]//TraditionalForm=