적분 변환 EntityStore
적분 변환은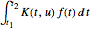 
의 형태의 적분에 의해 함수 
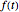를 다른 함수 
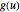에 매핑하는 수학 작업이며, 
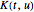는 이때 커널로 인지되어 있습니다. 적분 변환은 신호처리, 메디컬 이미징, 확률 이론 등 다양한 분야에서 매우 중요한 역할을 차지합니다. 여기서는 특성의 중요 변환을 담은 엔티티 스토어의 구축에 관해 알아봅니다.
엔티티 스토어는 EntityStore 데이터 구조 내의 적분 변환 중 가장 중요한 특성을 기록하여 수동으로 코딩 할 수있습니다.
In[1]:=
EntityStore[<|
"Types" -> <|
"IntegralTransform" -> <|
"Entities" -> <|
"ExponentialFourierTransform" -> <|
"Label" -> "exponential Fourier transform",
"StandardName" -> "ExponentialFourierTransform",
"StandardNotation" -> Hold[f[t]],
"Definition" -> Inactive[FourierTransform][f[t], t, z] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\)
Inactive[Integrate][
E^(I t z) f[t], {t, -\[Infinity], \[Infinity]}]/Sqrt[
2 \[Pi]],
"GeneralProperties" -> <|
"Linearity" -> {Inactive[FourierTransform][
a f[t] + b g[t], t, z] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\)
a Inactive[FourierTransform][f[t], t, z] +
b Inactive[FourierTransform][g[t], t, z],
Inactive[FourierTransform][f[t], t, z] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\)
Inactive[FourierTransform][f[-t] UnitStep[t], t, -z] +
Inactive[FourierTransform][f[t] UnitStep[t], t, z]},
"Reflection" -> {Inactive[FourierTransform][f[-t], t,
z] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, -z]},
"Dilation" -> {ConditionalExpression[
Inactive[FourierTransform][f[a t], t, z] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, z/a]/Abs[a],
a \!\(\*
TagBox["\[Element]",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"\[Element]"]\) Reals && a \!\(\*
TagBox["!=",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"!="]\) 0]},
"Shifting or translation" -> {ConditionalExpression[
Inactive[FourierTransform][f[-a + t], t, z] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\) E^(I a z) Inactive[FourierTransform][f[t], t, z],
a \!\(\*
TagBox["\[Element]",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"\[Element]"]\) Reals]}|>|>|>|>|>|>]Out[1]=
다음의 CloudObject에서 더욱 완전한 버전을 찾을 수 있습니다.
In[2]:=
itstore =
CloudGet[CloudObject[
"https://www.wolframcloud.com/objects/c21b356b-607a-406c-af91-\
5088f435fe99"]]Out[2]=
이 세션을 위해 스토어를 등록합니다.
In[3]:=
PrependTo[$EntityStores, itstore];스토어의 엔티티를 살펴봅니다.
In[4]:=
EntityValue["IntegralTransform", "Entities"]Out[4]=
새로운 변환을 추가합니다.
In[5]:=
Entity["IntegralTransform", "HilbertTransform"]["Label"] =
"Hilbert transform";
Entity["IntegralTransform", "HilbertTransform"]["Definition"] =
Inactive[HilbertTransform][f[t], t, x] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\)
1/\[Pi] Inactive[Integrate][f[t]/(
t - x), {t, -\[Infinity], \[Infinity]}, PrincipalValue -> True,
Assumptions -> x \!\(\*
TagBox["\[Element]",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"\[Element]"]\) Reals];적분 변환을 위해 현재 사용 가능한 특성을 반환합니다.
In[6]:=
EntityValue["IntegralTransform", "Properties"]Out[6]=
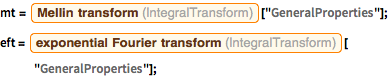
지수 푸리에 (Fourier) 변환과 멜린 (Mellin) 변환의 정의를 꺼냅니다.
In[7]:=
EntityValue[
Entity["IntegralTransform", "LaplaceTransform"], "Definition"]Out[7]=
In[8]:=
EntityValue[
Entity["IntegralTransform", "MellinTransform"], "Definition"]Out[8]=
대응하는 내장 함수가 반환한 결과 식과 비교합니다.
In[9]:=
Activate[EntityValue[Entity["IntegralTransform", "LaplaceTransform"],
"Definition"][[2]] /. f :> Function[t, ArcTan[t]]]Out[9]=
In[10]:=
LaplaceTransform[ArcTan[t], t, z]Out[10]=
Z-변환의 회선 특성을 표시합니다.
In[11]:=
Entity["IntegralTransform", "ZTransform"][
"GeneralProperties"]["Convolution"]Out[11]=
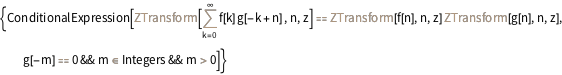
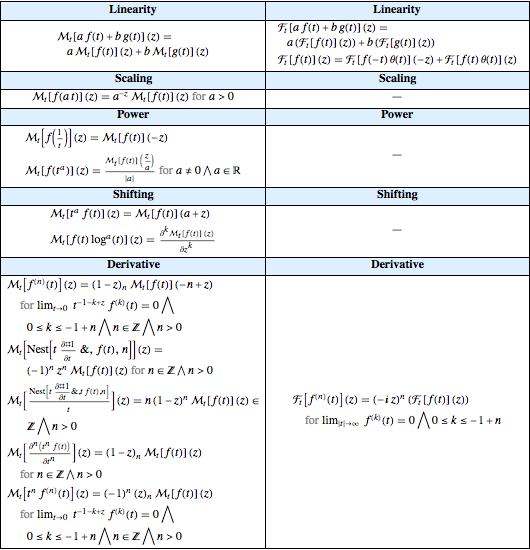
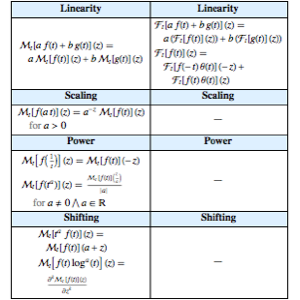
지수 푸리에 변환과 멜린 변환의 현재 저장되어 있는 특성을 비교합니다.
전체 Wolfram 언어 입력 표시하기
Out[14]//TraditionalForm=
