积分变换 EntityStore
积分变换是一种数学运算，它以形式为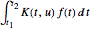 
的积分方法，将函数 
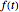映射到另一函数 
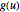，其中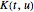 
称为核. 积分变换在信号处理、医学成像和概率论等众多研究领域占有中非常重要的地位. 这里展示了包含重要变换属性的实体库的构建过程.
通过在 EntityStore 数据结构中记录积分变换的重要属性，可以手动编码创建实体库.
In[1]:=
EntityStore[<|
"Types" -> <|
"IntegralTransform" -> <|
"Entities" -> <|
"ExponentialFourierTransform" -> <|
"Label" -> "exponential Fourier transform",
"StandardName" -> "ExponentialFourierTransform",
"StandardNotation" -> Hold[f[t]],
"Definition" -> Inactive[FourierTransform][f[t], t, z] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\)
Inactive[Integrate][
E^(I t z) f[t], {t, -\[Infinity], \[Infinity]}]/Sqrt[
2 \[Pi]],
"GeneralProperties" -> <|
"Linearity" -> {Inactive[FourierTransform][
a f[t] + b g[t], t, z] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\)
a Inactive[FourierTransform][f[t], t, z] +
b Inactive[FourierTransform][g[t], t, z],
Inactive[FourierTransform][f[t], t, z] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\)
Inactive[FourierTransform][f[-t] UnitStep[t], t, -z] +
Inactive[FourierTransform][f[t] UnitStep[t], t, z]},
"Reflection" -> {Inactive[FourierTransform][f[-t], t,
z] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, -z]},
"Dilation" -> {ConditionalExpression[
Inactive[FourierTransform][f[a t], t, z] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, z/a]/Abs[a],
a \!\(\*
TagBox["\[Element]",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"\[Element]"]\) Reals && a \!\(\*
TagBox["!=",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"!="]\) 0]},
"Shifting or translation" -> {ConditionalExpression[
Inactive[FourierTransform][f[-a + t], t, z] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\) E^(I a z) Inactive[FourierTransform][f[t], t, z],
a \!\(\*
TagBox["\[Element]",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"\[Element]"]\) Reals]}|>|>|>|>|>|>]Out[1]=
更复杂的版本可以从以下 CloudObject 中提取.
In[2]:=
itstore =
CloudGet[CloudObject[
"https://www.wolframcloud.com/objects/c21b356b-607a-406c-af91-\
5088f435fe99"]]Out[2]=
注册该部分数据库.
In[3]:=
PrependTo[$EntityStores, itstore];查看数据库中的实体.
In[4]:=
EntityValue["IntegralTransform", "Entities"]Out[4]=
添加新的变换.
In[5]:=
Entity["IntegralTransform", "HilbertTransform"]["Label"] =
"Hilbert transform";
Entity["IntegralTransform", "HilbertTransform"]["Definition"] =
Inactive[HilbertTransform][f[t], t, x] \!\(\*
TagBox["==",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"=="]\)
1/\[Pi] Inactive[Integrate][f[t]/(
t - x), {t, -\[Infinity], \[Infinity]}, PrincipalValue -> True,
Assumptions -> x \!\(\*
TagBox["\[Element]",
"InactiveToken",
BaseStyle->"Inactive",
SyntaxForm->"\[Element]"]\) Reals];对积分变换返回当前可用的属性.
In[6]:=
EntityValue["IntegralTransform", "Properties"]Out[6]=
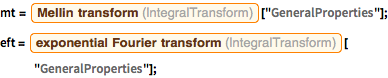
提取指数傅里叶和梅林变换的定义.
In[7]:=
EntityValue[
Entity["IntegralTransform", "LaplaceTransform"], "Definition"]Out[7]=
In[8]:=
EntityValue[
Entity["IntegralTransform", "MellinTransform"], "Definition"]Out[8]=
与对应的内置函数返回的表达式比较.
In[9]:=
Activate[EntityValue[Entity["IntegralTransform", "LaplaceTransform"],
"Definition"][[2]] /. f :> Function[t, ArcTan[t]]]Out[9]=
In[10]:=
LaplaceTransform[ArcTan[t], t, z]Out[10]=
显示 Z-变换的卷积属性.
In[11]:=
Entity["IntegralTransform", "ZTransform"][
"GeneralProperties"]["Convolution"]Out[11]=
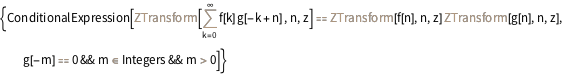
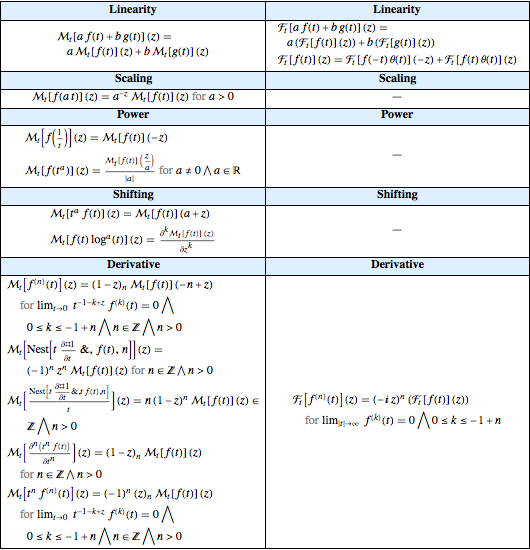
与当前存储的傅里叶和梅林变换属性对比.
显示完整的 Wolfram 语言输入
Out[14]//TraditionalForm=
