Wolfram Language™

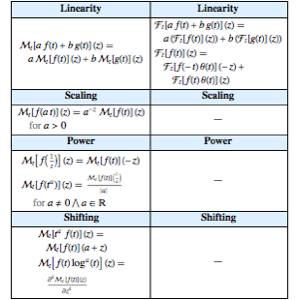
Réseau de dérivées de fonctions spéciales

Wolfram Language contient plus de 300 fonctions mathématiques intégrées. Considérez l'opération de différenciation appliquée à chacune de ces fonctions. Dans la plupart des cas, une ou plusieurs nouvelles fonctions apparaissent dans les dérivées obtenues. La quantification des connexions permet d'étudier de manière intéressante la relation entre les symboles et les opérations qu'ils subissent. En particulier, l'exemple suivant illustre le réseau qui découle de la différenciation d'ordre inférieur.

Comme nous l'avons appris en calcul élémentaire, la différenciation du logarithme naturel donne la fonction réciproque.

In[1]:=

D[Log[x], x]

Out[1]=

D'autre part, pour certaines fonctions, une dérivée peut être exprimée directement par la fonction d'origine.

In[2]:=

D[ProductLog[x], x]

Out[2]=

La propriété "LowOrderDerivatives" de MathematicalFunctionData offre un accès rapide et pratique à toutes les dérivées.

In[3]:=

Entity["MathematicalFunction", "EllipticF"][ EntityProperty["MathematicalFunction", "LowOrderDerivatives"]] // TraditionalForm

Out[3]//TraditionalForm=

Rassemblez toutes les fonctions et leurs modèles d'arguments afin d'identifier la fonction après différenciation. (Pour éviter les occurrences courantes de puissances, ne cherchez pas la fonction puissance et racine carrée). Par exemple, sur la base de l'identité , la fonction Sec implique les fonctions Tan ainsi qu'elle-même, ce qui donne lieu à deux connexions.

In[4]:=

allFunctions = DeleteCases[MathematicalFunctionData[], Entity["MathematicalFunction", "Sqrt"] | Entity["MathematicalFunction", "Power"]];

In[5]:=

patts = EntityValue[allFunctions, EntityProperty["MathematicalFunction", "ArgumentPattern"]];

In[6]:=

toPattern[p_] := Activate[Hold @@ { p /. Verbatim[PatternTest][a_, b_] :> a /. Verbatim[Alternatives][a_, __] :> a /. Verbatim[Blank][_] :> _}]

In[7]:=

pairs = {#1, toPattern[#2]} & @@@ Transpose[{allFunctions, patts}];

In[8]:=

(identify[#2] = #1) & @@@ pairs;

In[9]:=

makeConnection[f1_, id_] := Module[{indices, heldSubexpressions, f2List, \[ScriptCapitalF]\[GothicCapitalF]}, indices = Quiet[Cases[ MapIndexed[\[ScriptCapitalF]\[GothicCapitalF], id, {0, \[Infinity]}], _\[ScriptCapitalF]\[GothicCapitalF], \ \[Infinity]][[All, -1]]]; heldSubexpressions = Union[Extract[id, indices, Hold]]; f2List = Union[Last /@ DeleteCases[({#1, identify[#1]} & /@ heldSubexpressions), {_, _identify}]]; {f1 \[DirectedEdge] #, id /. HoldPattern[Function[_, Inactivate[x_]]] :> HoldForm[x]} & /@ f2List]

In[10]:=

makeConnection[Entity["MathematicalFunction", "Sec"] , Function[{x}, Inactivate[D[Sec[x], x] == Sec[x] Tan[x]]]]

Out[10]=

Analysez toutes les dérivées, éliminez toutes les boucles triviales dans les graphiques résultants et visualisez la structure du graphe obtenu.

In[11]:=

\[Lambda]F = Length[allFunctions]; Monitor[ allConnections = Table[ fD = allFunctions[[\[ScriptJ]]]; derivatives = Activate[ allFunctions[[\[ScriptJ]]][ EntityProperty["MathematicalFunction", "LowOrderDerivatives"]] /. HoldPattern[Power[E, z_]] :> Exp[z]]; connections = If[derivatives === Missing["NotAvailable"], {}, {#[[1, 1]], SortBy[#[[All, -1]], LeafCount]} & /@ GatherBy[ Flatten[makeConnection[fD, #] & /@ derivatives, 1] // Union, First]], {\[ScriptJ], \[Lambda]F}];, Row[{"function ", \[ScriptJ], " of ", \[Lambda]F, ": ", fD}]];

In[12]:=

gr = Graph[Flatten[allConnections, 1][[All, 1]]]

Out[12]=

Comptez le nombre de connexions.

In[13]:=

Flatten[allConnections, 1] // Length

Out[13]=

Trouvez des boucles automatiques.

In[14]:=

selfLoops = Select[ConnectedComponents[ Graph[Flatten[allConnections /. DirectedEdge -> UndirectedEdge, 1][[All, 1]]]], Length[#] == 1 &]

Out[14]=

Trouvez les groupes de fonctions qui sont fermés sous différenciation et visualisez-les sous forme de graphes étiquetés.

In[15]:=

smallLoops = Select[ConnectedComponents[ Graph[Flatten[allConnections /. DirectedEdge -> UndirectedEdge, 1][[All, 1]]]], 1 < Length[#] < 20 &];

In[16]:=

Graph[Select[Flatten[allConnections, 1], MemberQ[#, Alternatives @@ Flatten[smallLoops], \[Infinity]] &][[ All, 1]], VertexLabels -> ((# -> MapAt[Nothing &, CommonName[#], {{1, 1}}]) & /@ Union[Flatten[smallLoops]])]

Out[16]=

La plupart des fonctions font partie de la composante géante du graphique. Passez la souris sur les sommets pour voir les fonctions et sur les arêtes pour voir les dérivées qui relient les fonctions.

In[17]:=

allConnectionsRest = Select[Flatten[allConnections, 1], FreeQ[#, Alternatives @@ Flatten[{selfLoops, smallLoops}], \[Infinity]] &];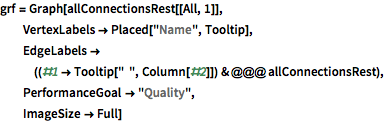

In[18]:=

grf = Graph[allConnectionsRest[[All, 1]], VertexLabels -> Placed["Name", Tooltip], EdgeLabels -> ((#1 -> Tooltip[" ", Column[#2]]) & @@@ allConnectionsRest), PerformanceGoal -> "Quality", ImageSize -> Full]

Out[18]=

La division du graphe en communautés fait apparaître les fonctions elliptiques, les fonctions hypergéométriques, les fonctions à fenêtre, les fonctions zêta et quelques autres groupes de fonctions.

In[19]:=

CommunityGraphPlot[grf, FindGraphCommunities[grf, Method -> "Modularity"]]

Out[19]=