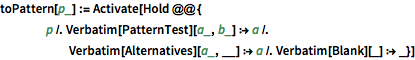特殊函数导数网络: Wolfram 语言 11 的新功能

‹›

特殊函数导数网络

Wolfram 语言包含了超过 300 种的内置数学函数. 考虑将微分操作应用于每个函数. 大多数情况下，导数结果会出现一个或多个函数. 对连接的量化提供了符号和对其的操作之间关系的有趣研究. 特别是，以下范例导出了从低阶微分生成的网络.

与初等微积分中学到的相同，对自然对数的微分会给出一个倒数函数.

In[1]:=

D[Log[x], x]

Out[1]=

另一方面，对于某些特定函数，导数可以直接用原来的函数表示.

In[2]:=

D[ProductLog[x], x]

Out[2]=

的 MathematicalFunctionData 的 "LowOrderDerivatives" 属性提供快速方便的方法访问全部导数.

In[3]:=

Entity["MathematicalFunction", "EllipticF"][
  EntityProperty["MathematicalFunction", 
   "LowOrderDerivatives"]] // TraditionalForm

Out[3]//TraditionalForm=

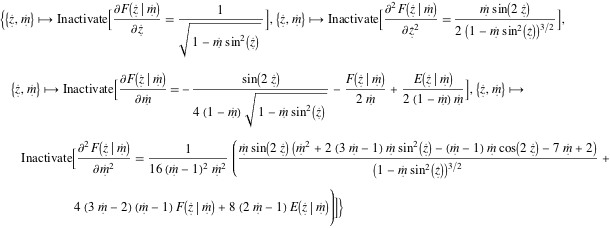
收集所有函数和其参数特征，从而在微分后对其进行识别（为避免常见的指数的出现，不要寻找指数和平方根函数）.比如，基于恒等式，函数 Sec 包含函数 Tan 以及其自身，结果产生两个连接.

显示完整的 Wolfram 语言输入

In[4]:=

allFunctions = 
  DeleteCases[MathematicalFunctionData[], 
   Entity["MathematicalFunction", "Sqrt"] | 
    Entity["MathematicalFunction", "Power"]];

In[5]:=

patts = EntityValue[allFunctions, 
   EntityProperty["MathematicalFunction", "ArgumentPattern"]];

In[6]:=

toPattern[p_] := Activate[Hold @@ {
    p /. Verbatim[PatternTest][a_, b_] :> a /. 
      Verbatim[Alternatives][a_, __] :> a /. Verbatim[Blank][_] :> _}]

In[7]:=

pairs = {#1, toPattern[#2]} & @@@ Transpose[{allFunctions, patts}];

In[8]:=

(identify[#2] = #1) & @@@ pairs;

In[9]:=

makeConnection[f1_, id_] :=
 
 Module[{indices, heldSubexpressions, 
   f2List, \[ScriptCapitalF]\[GothicCapitalF]},
  indices = 
   Quiet[Cases[
      MapIndexed[\[ScriptCapitalF]\[GothicCapitalF], 
       id, {0, \[Infinity]}], _\[ScriptCapitalF]\[GothicCapitalF], \
\[Infinity]][[All, -1]]];
  heldSubexpressions = Union[Extract[id, indices, Hold]];
  f2List = 
   Union[Last /@ 
     DeleteCases[({#1, identify[#1]} & /@ 
        heldSubexpressions), {_, _identify}]];
  {f1 \[DirectedEdge] #, 
     id /. HoldPattern[Function[_, Inactivate[x_]]] :> 
       HoldForm[x]} & /@ f2List]

In[10]:=

makeConnection[Entity["MathematicalFunction", "Sec"] , 
 Function[{x}, Inactivate[D[Sec[x], x] == Sec[x] Tan[x]]]]

Out[10]=

分析所有导数，除去图形中所有不重要的自循环，并可视化产生的图形结构.

显示完整的 Wolfram 语言输入

In[11]:=

\[Lambda]F = Length[allFunctions];
Monitor[
  allConnections = Table[
     fD = allFunctions[[\[ScriptJ]]];
     derivatives = 
      Activate[
       allFunctions[[\[ScriptJ]]][
         EntityProperty["MathematicalFunction", 
          "LowOrderDerivatives"]] /. 
        HoldPattern[Power[E, z_]] :> Exp[z]];
     connections =
      If[derivatives === Missing["NotAvailable"], {},
       {#[[1, 1]], SortBy[#[[All, -1]], LeafCount]} & /@ 
        GatherBy[
         Flatten[makeConnection[fD, #] & /@ derivatives, 1] // Union, 
         First]],
     {\[ScriptJ], \[Lambda]F}];, 
  Row[{"function ", \[ScriptJ], " of ", \[Lambda]F, ": ", fD}]];

In[12]:=

gr = Graph[Flatten[allConnections, 1][[All, 1]]]

Out[12]=

计算连接数目.

In[13]:=

Flatten[allConnections, 1] // Length

Out[13]=

找出自循环.

In[14]:=

selfLoops = 
 Select[ConnectedComponents[
   Graph[Flatten[allConnections /. DirectedEdge -> UndirectedEdge, 
      1][[All, 1]]]], Length[#] == 1 &]

Out[14]=

找出微分后闭合的函数组，并用有标签的图形进行可视化.

显示完整的 Wolfram 语言输入

In[15]:=

smallLoops = 
  Select[ConnectedComponents[
    Graph[Flatten[allConnections /. DirectedEdge -> UndirectedEdge, 
       1][[All, 1]]]], 1 < Length[#] < 20 &];

In[16]:=

Graph[Select[Flatten[allConnections, 1], 
   MemberQ[#, Alternatives @@ Flatten[smallLoops], \[Infinity]] &][[
  All, 1]],
 VertexLabels -> ((# -> MapAt[Nothing &, CommonName[#], {{1, 1}}]) & /@
     Union[Flatten[smallLoops]])]

Out[16]=

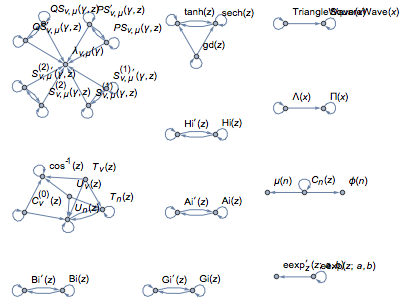
大多数的函数是图形的巨大分支的一部分. 将鼠标放置在顶点上查看函数，并在边上查看与函数相连接的导数.

In[17]:=

allConnectionsRest = 
  Select[Flatten[allConnections, 1], 
   FreeQ[#, 
     Alternatives @@ 
      Flatten[{selfLoops, smallLoops}], \[Infinity]] &];

In[18]:=

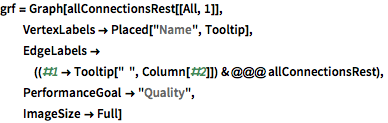
grf = Graph[allConnectionsRest[[All, 1]],
  VertexLabels -> Placed["Name", Tooltip],
  EdgeLabels -> ((#1 -> Tooltip["  ", Column[#2]]) & @@@ 
     allConnectionsRest),
  PerformanceGoal -> "Quality",
  ImageSize -> Full]

Out[18]=

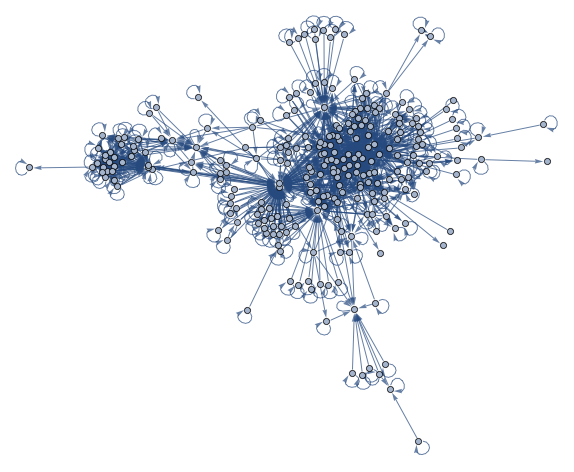
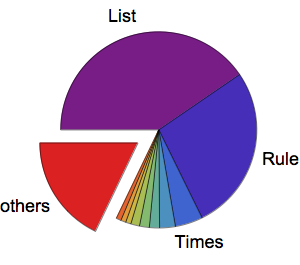
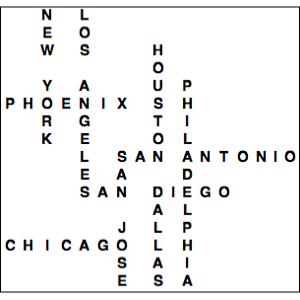
将图形分割为社区分别显示椭圆函数、超几何函数、窗口函数、泽塔函数和其他函数组.

In[19]:=

CommunityGraphPlot[grf, 
 FindGraphCommunities[grf, Method -> "Modularity"]]

Out[19]=

Wolfram 语言™

特殊函数导数网络

相关范例