Wolfram Mathematica

Special Function Derivative Network

The Wolfram Language contains more than 300 built-in mathematical functions. Consider the operation of differentiation applied to each of these functions. In most cases, one or more new functions appear in the resulting derivatives. Quantifying the connections gives an interesting study on the relationship between symbols and operations on them. In particular, the following example derives the network that arises from low‐order differentiation.

As learned in elementary calculus, differentiating the natural logarithm gives the reciprocal function.

In[1]:=

D[Log[x], x]

Out[1]=

On the other hand, for certain functions, a derivative can be expressed directly through the original function.

In[2]:=

D[ProductLog[x], x]

Out[2]=

The "LowOrderDerivatives" property of MathematicalFunctionData provides quick and convenient access to all derivatives.

In[3]:=

Entity["MathematicalFunction", "EllipticF"][ EntityProperty["MathematicalFunction", "LowOrderDerivatives"]] // TraditionalForm

Out[3]//TraditionalForm=

Collect all functions and their argument patterns in order to identify the function after differentiation. (To avoid common occurrences of powers, do not look for the power and square root function.) For example, based on the identity , the function Sec involves the functions Tan as well as itself, resulting in two connections.

In[4]:=

allFunctions = DeleteCases[MathematicalFunctionData[], Entity["MathematicalFunction", "Sqrt"] | Entity["MathematicalFunction", "Power"]];

In[5]:=

patts = EntityValue[allFunctions, EntityProperty["MathematicalFunction", "ArgumentPattern"]];

In[6]:=

toPattern[p_] := Activate[Hold @@ { p /. Verbatim[PatternTest][a_, b_] :> a /. Verbatim[Alternatives][a_, __] :> a /. Verbatim[Blank][_] :> _}]

In[7]:=

pairs = {#1, toPattern[#2]} & @@@ Transpose[{allFunctions, patts}];

In[8]:=

(identify[#2] = #1) & @@@ pairs;

In[9]:=

makeConnection[f1_, id_] := Module[{indices, heldSubexpressions, f2List, \[ScriptCapitalF]\[GothicCapitalF]}, indices = Quiet[Cases[ MapIndexed[\[ScriptCapitalF]\[GothicCapitalF], id, {0, \[Infinity]}], _\[ScriptCapitalF]\[GothicCapitalF], \ \[Infinity]][[All, -1]]]; heldSubexpressions = Union[Extract[id, indices, Hold]]; f2List = Union[Last /@ DeleteCases[({#1, identify[#1]} & /@ heldSubexpressions), {_, _identify}]]; {f1 \[DirectedEdge] #, id /. HoldPattern[Function[_, Inactivate[x_]]] :> HoldForm[x]} & /@ f2List]

In[10]:=

makeConnection[Entity["MathematicalFunction", "Sec"] , Function[{x}, Inactivate[D[Sec[x], x] == Sec[x] Tan[x]]]]

Out[10]=

Analyze all derivatives, eliminate all trivial self-loops in the resulting graphs, and visualize the resulting graph structure.

In[11]:=

\[Lambda]F = Length[allFunctions]; Monitor[ allConnections = Table[ fD = allFunctions[[\[ScriptJ]]]; derivatives = Activate[ allFunctions[[\[ScriptJ]]][ EntityProperty["MathematicalFunction", "LowOrderDerivatives"]] /. HoldPattern[Power[E, z_]] :> Exp[z]]; connections = If[derivatives === Missing["NotAvailable"], {}, {#[[1, 1]], SortBy[#[[All, -1]], LeafCount]} & /@ GatherBy[ Flatten[makeConnection[fD, #] & /@ derivatives, 1] // Union, First]], {\[ScriptJ], \[Lambda]F}];, Row[{"function ", \[ScriptJ], " of ", \[Lambda]F, ": ", fD}]];

In[12]:=

gr = Graph[Flatten[allConnections, 1][[All, 1]]]

Out[12]=

Count the number of connections.

In[13]:=

Flatten[allConnections, 1] // Length

Out[13]=

Find self-loops.

In[14]:=

selfLoops = Select[ConnectedComponents[ Graph[Flatten[allConnections /. DirectedEdge -> UndirectedEdge, 1][[All, 1]]]], Length[#] == 1 &]

Out[14]=

Find the groups of functions that are closed under differentiation and visualize as labeled graphs.

In[15]:=

smallLoops = Select[ConnectedComponents[ Graph[Flatten[allConnections /. DirectedEdge -> UndirectedEdge, 1][[All, 1]]]], 1 < Length[#] < 20 &];

In[16]:=

Graph[Select[Flatten[allConnections, 1], MemberQ[#, Alternatives @@ Flatten[smallLoops], \[Infinity]] &][[ All, 1]], VertexLabels -> ((# -> MapAt[Nothing &, CommonName[#], {{1, 1}}]) & /@ Union[Flatten[smallLoops]])]

Out[16]=

Most functions are part of the giant component of the graph. Mouse over the vertices to see the functions and over the edges to see the derivatives that connect the functions.

In[17]:=

allConnectionsRest = Select[Flatten[allConnections, 1], FreeQ[#, Alternatives @@ Flatten[{selfLoops, smallLoops}], \[Infinity]] &];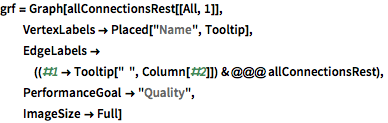

In[18]:=

grf = Graph[allConnectionsRest[[All, 1]], VertexLabels -> Placed["Name", Tooltip], EdgeLabels -> ((#1 -> Tooltip[" ", Column[#2]]) & @@@ allConnectionsRest), PerformanceGoal -> "Quality", ImageSize -> Full]

Out[18]=

Splitting the graph into communities shows elliptic functions, hypergeometric functions, window functions, zeta functions, and a few more groups of functions.

In[19]:=

CommunityGraphPlot[grf, FindGraphCommunities[grf, Method -> "Modularity"]]

Out[19]=