Wolfram Language™

Évaluez un sac de pièces de monnaie

Un sac contenant des pièces de monnaie américaines neuves a été volé dans une banque. Sans ouvrir le sac, que peut-on dire de la valeur monétaire de son contenu ? Le poids du sac est une caractéristique physique évidente et facile à mesurer. Dans l'hypothèse d'un sac de pièces d'une livre, combinez le savoir-faire de la base de connaissances de Wolfram en matière de monnaies et sa capacité intégrée à résoudre des équations linéaires pour étudier la valeur attendue du butin.

Pour commencer, renvoyez une liste de pièces de monnaie américaines en circulation au moyen d'une classe d'entités implicitement définie.

In[1]:=

EntityClass["CurrencyDenomination", {EntityProperty[ "CurrencyDenomination", "IssuingCountry"] -> Entity["Country", "UnitedStates"], EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]

Out[1]=

Agrandissez la classe d'entité implicitement définie en cliquant sur le [+], trouvez les membres de cette classe et classez-les par valeur.

In[2]:=

coinsUS = EntityList[ EntityClass[ "CurrencyDenomination", { EntityProperty[ "CurrencyDenomination", "IssuingCountry"] -> Entity[ "Country", "UnitedStates"], EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]] // SortBy[#[EntityProperty["CurrencyDenomination", "Value"]] &]

Out[2]=

Réalisez un collage d'images de pièces de monnaie.

In[3]:=

ImageCollage[ EntityValue[coinsUS, EntityProperty["CurrencyDenomination", "Image"]], Background -> White]

Out[3]=

Résumez les propriétés des pièces de monnaie dans un tableau.

In[4]:=

TextGrid[{ImageResize[#2, 60], #1, Row[Riffle[#3, Style[" | ", Gray]]]} & @@@ EntityValue[ coinsUS, {EntityProperty["CurrencyDenomination", "Entity"], EntityProperty["CurrencyDenomination", "Image"], EntityProperty["CurrencyDenomination", "PeopleOnCurrency"]}], Alignment -> {Left, Center}, Dividers -> All] // TraditionalForm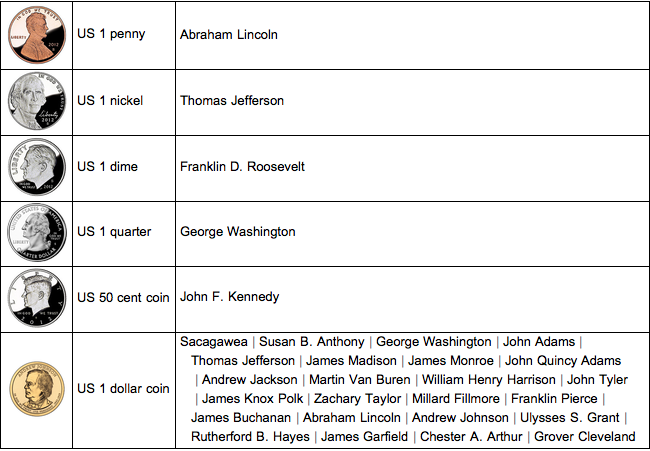

Out[4]//TraditionalForm=

Obtenez les dénominations des pièces (en centimes) et les masses (en grammes) et convertissez les masses en nombres rationnels.

In[5]:=

{values, masses} = Transpose[EntityValue[coinsUS, {"Value", "Weight"}]]

Out[5]=

In[6]:=

coinsandweights = Transpose[{ QuantityMagnitude[UnitConvert[values, "USCents"]], Rationalize[QuantityMagnitude[N[UnitConvert[masses, "Grams"]]]] }]

Out[6]=

In[7]:=

lcm = LCM @@ Denominator[Rationalize[coinsandweights][[All, 2]]];

In[8]:=

rationalcoinweights = lcm #2 & @@@ Rationalize[coinsandweights]

Out[8]=

Trouvez toutes les distributions de pièces compatibles avec une mesure de poids d'une livre avec une mesure d'erreur de ± 0,1% (en supposant que le sac lui-même contribue de manière négligeable).

In[9]:=

meanWeight = QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]];

In[10]:=

error = Normal[Quantity[0.1, "Percent"]];

In[11]:=

{minScaledWeight, maxScaledWeight} = {Floor[lcm meanWeight (1 - error/2)], Ceiling[lcm meanWeight (1 + error/2)]}

Out[11]=

Utilisez FrobeniusSolve pour déterminer toutes les collections de pièces possibles donnant le poids total requis.

In[12]:=

allSolutions = Monitor[ Table[fb = FrobeniusSolve[rationalcoinweights, scaledweight], {scaledweight, minScaledWeight, maxScaledWeight}], Row[{NumberForm[ 100. (scaledweight - minScaledWeight)/(maxScaledWeight - minScaledWeight), {4, 1}, "NumberPadding" -> {" ", "0"}], "%: ", Length[fb], " solutions"}] ];

In[13]:=

Flatten[allSolutions, 1] // Length

Out[13]=

Trouvez les valeurs minimale, médiane, moyenne et maximale de la valeur monétaire totale des pièces du sac (en supposant que toutes les combinaisons ont la même probabilité).

In[14]:=

coins = coinsandweights[[All, 1]];

In[15]:=

dollarValues = (coins.#/100.) & /@ Flatten[allSolutions, 1];

In[16]:=

TextGrid[With[{stats = {Min, Median, Mean, Max}}, Transpose[{stats, NumberForm[Quantity[#, "USDollars"], {\[Infinity], 2}] & /@ Through[stats[dollarValues]]}]], Alignment -> {{Left, Decimal}}, Dividers -> All, Background -> {Automatic, {{LightBlue, None}}}] // TraditionalForm

Out[16]//TraditionalForm=

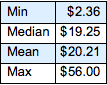
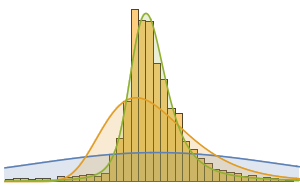
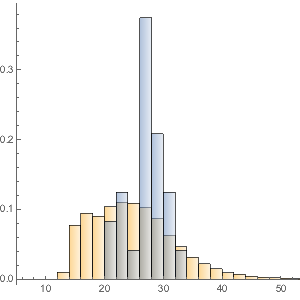
Faites un histogramme de la répartition de la valeur monétaire totale.

In[17]:=

Histogram[dollarValues, Automatic, "PDF", AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]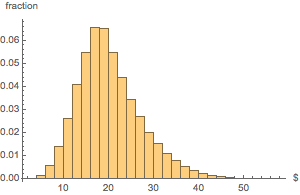

Out[17]=

La répartition du poids de tous les sacs est assez uniforme.

In[18]:=

weights = coinsandweights[[All, -1]]; lbg = QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]]; weightvalues = (weights.#)/lbg & /@ Flatten[allSolutions, 1];

In[19]:=

Histogram[weightvalues, 50, "PDF", AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]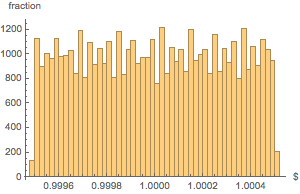

Out[19]=

Tracez la répartition du nombre de pièces.

In[20]:=

Histogram[Total /@ Flatten[allSolutions, 1], {5}]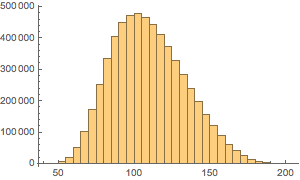

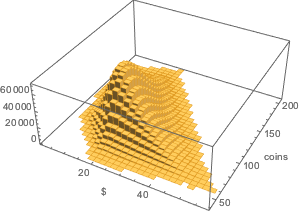
Out[20]=

Voici la répartition bivariée de la valeur monétaire en fonction du nombre de pièces dans le sac.

In[21]:=

Histogram3D[{coins.#/100., Total[#]} & /@ Flatten[allSolutions, 1], AxesLabel -> {Quantity[None, "USDollars"], "coins"}]

Out[21]=