一袋のコインの値

一袋のアメリカ合衆国コインが銀行から盗まれた．袋を開けずに中身の金額を語ることはできるだろうか．明らかで物理的な袋の特徴はその重さだろう．コインが入った重さ1ポンドの袋を仮定し，Wolfram Knowledgebaseの通貨についての情報と線形方程式を解く組込み機能を使って，盗まれたコインの期待される値を求めることができる．

まず，隠的に定義された実体クラスを使って現在出回っているアメリカ合衆国コインのリストを返す．

In[1]:=

EntityClass["CurrencyDenomination", {EntityProperty[ "CurrencyDenomination", "IssuingCountry"] -> Entity["Country", "UnitedStates"], EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]

Out[1]=

[+]をクリックして隠的に定義された実体クラスを拡張し，メンバーを求め，値によってソートする．

In[2]:=

coinsUS = EntityList[ EntityClass[ "CurrencyDenomination", { EntityProperty[ "CurrencyDenomination", "IssuingCountry"] -> Entity[ "Country", "UnitedStates"], EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]] // SortBy[#[EntityProperty["CurrencyDenomination", "Value"]] &]

Out[2]=

コインの画像のコラージュを作る．

In[3]:=

ImageCollage[ EntityValue[coinsUS, EntityProperty["CurrencyDenomination", "Image"]], Background -> White]

Out[3]=

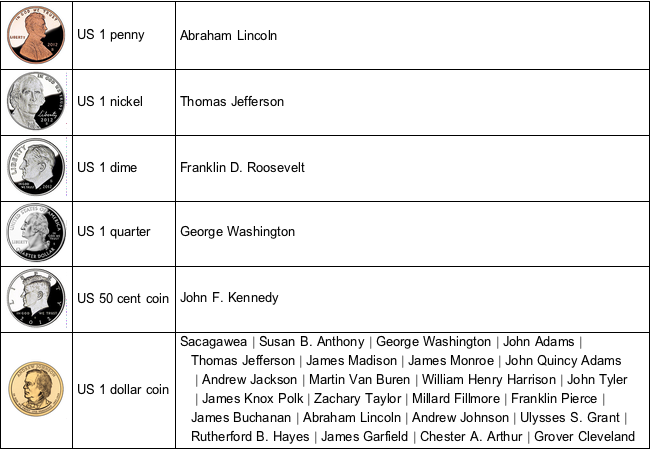
コインの特性を表にまとめる．

In[4]:=

TextGrid[{ImageResize[#2, 60], #1, Row[Riffle[#3, Style[" | ", Gray]]]} & @@@ EntityValue[ coinsUS, {EntityProperty["CurrencyDenomination", "Entity"], EntityProperty["CurrencyDenomination", "Image"], EntityProperty["CurrencyDenomination", "PeopleOnCurrency"]}], Alignment -> {Left, Center}, Dividers -> All] // TraditionalForm

Out[4]//TraditionalForm=

コインの金額（セント）と質量（グラム）を求め，質量を有理数に変換する．

In[5]:=

{values, masses} = Transpose[EntityValue[coinsUS, {"Value", "Weight"}]]

Out[5]=

In[6]:=

coinsandweights = Transpose[{ QuantityMagnitude[UnitConvert[values, "USCents"]], Rationalize[QuantityMagnitude[N[UnitConvert[masses, "Grams"]]]] }]

Out[6]=

In[7]:=

lcm = LCM @@ Denominator[Rationalize[coinsandweights][[All, 2]]];

In[8]:=

rationalcoinweights = lcm #2 & @@@ Rationalize[coinsandweights]

Out[8]=

全体で重さが1ポンドになるコインの組合せ分布すべてを± 0.1%の誤差で求める（袋の重さは無視できるものとする）．

In[9]:=

meanWeight = QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]];

In[10]:=

error = Normal[Quantity[0.1, "Percent"]];

In[11]:=

{minScaledWeight, maxScaledWeight} = {Floor[lcm meanWeight (1 - error/2)], Ceiling[lcm meanWeight (1 + error/2)]}

Out[11]=

FrobeniusSolveを使って，必要な重さになる可能なすべてのコイン集合を決定する．

In[12]:=

allSolutions = Monitor[ Table[fb = FrobeniusSolve[rationalcoinweights, scaledweight], {scaledweight, minScaledWeight, maxScaledWeight}], Row[{NumberForm[ 100. (scaledweight - minScaledWeight)/(maxScaledWeight - minScaledWeight), {4, 1}, "NumberPadding" -> {" ", "0"}], "%: ", Length[fb], " solutions"}] ];

In[13]:=

Flatten[allSolutions, 1] // Length

Out[13]=

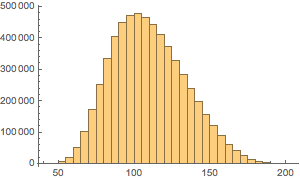
袋の中のコインの最小値，中央値，平均値，最大値を求める（どの組合せも同程度に起こり得ると仮定する）．

In[14]:=

coins = coinsandweights[[All, 1]];

In[15]:=

dollarValues = (coins.#/100.) & /@ Flatten[allSolutions, 1];

In[16]:=

TextGrid[With[{stats = {Min, Median, Mean, Max}}, Transpose[{stats, NumberForm[Quantity[#, "USDollars"], {\[Infinity], 2}] & /@ Through[stats[dollarValues]]}]], Alignment -> {{Left, Decimal}}, Dividers -> All, Background -> {Automatic, {{LightBlue, None}}}] // TraditionalForm

Out[16]//TraditionalForm=

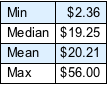
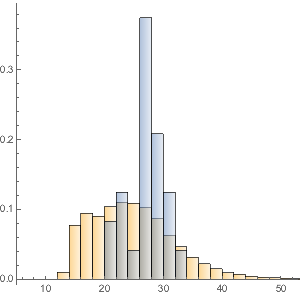
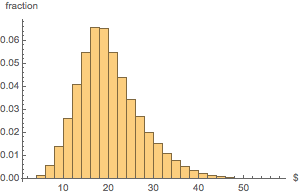
合計金額の分布のヒストグラムを作る．

In[17]:=

Histogram[dollarValues, Automatic, "PDF", AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]

Out[17]=

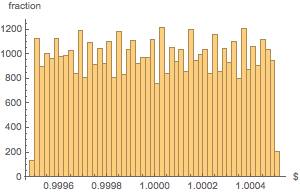
すべての袋の重さの分布は，かなり一様である．

In[18]:=

weights = coinsandweights[[All, -1]]; lbg = QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]]; weightvalues = (weights.#)/lbg & /@ Flatten[allSolutions, 1];

In[19]:=

Histogram[weightvalues, 50, "PDF", AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]

Out[19]=

コインの数の分布をプロットする．

In[20]:=

Histogram[Total /@ Flatten[allSolutions, 1], {5}]

Out[20]=

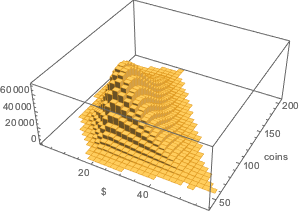
金額と袋の中のコイン数の二変量分布：

In[21]:=

Histogram3D[{coins.#/100., Total[#]} & /@ Flatten[allSolutions, 1], AxesLabel -> {Quantity[None, "USDollars"], "coins"}]

Out[21]=