估计一袋硬币的价值: Wolfram 语言 11 的新功能

估计一袋硬币的价值

一袋新美国硬币从银行被盗走. 在不代开袋子的条件下，其中所含的货币价值是多少？一个明显并简单测量的物理特性是袋子的重量. 假设一袋 1 磅重的硬币，并结合 Wolfram Knowledgebase 中关于货币的知识，以及求解线性方程式的内置功能来研究盗窃预期值.

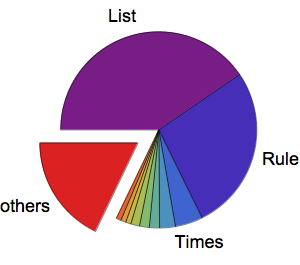
开始之前，根据一个隐式定义的实体类返回目前流通的美国硬币列表.

In[1]:=

EntityClass["CurrencyDenomination", {EntityProperty[
    "CurrencyDenomination", "IssuingCountry"] -> 
   Entity["Country", "UnitedStates"], 
  EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]

Out[1]=

单击 [+] 打开隐式定义的实体类型，找出其中成员并按价值排序.

In[2]:=

coinsUS = EntityList[
EntityClass[
   "CurrencyDenomination", {
    EntityProperty[
      "CurrencyDenomination", "IssuingCountry"] -> Entity[
      "Country", "UnitedStates"], 
     EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]] // 
  SortBy[#[EntityProperty["CurrencyDenomination", "Value"]] &]

Out[2]=

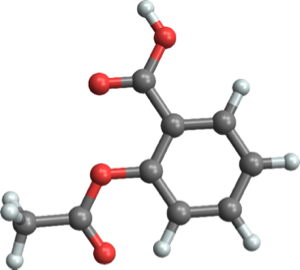
创建一张硬币图像的拼贴图.

In[3]:=

ImageCollage[
 EntityValue[coinsUS, 
  EntityProperty["CurrencyDenomination", "Image"]], 
 Background -> White]

Out[3]=

在表格中总结硬币属性.

In[4]:=

TextGrid[{ImageResize[#2, 60], #1, 
     Row[Riffle[#3, Style[" | ", Gray]]]} & @@@ 
   EntityValue[
    coinsUS, {EntityProperty["CurrencyDenomination", "Entity"], 
     EntityProperty["CurrencyDenomination", "Image"], 
     EntityProperty["CurrencyDenomination", "PeopleOnCurrency"]}], 
  Alignment -> {Left, Center}, Dividers -> All] // TraditionalForm

Out[4]//TraditionalForm=

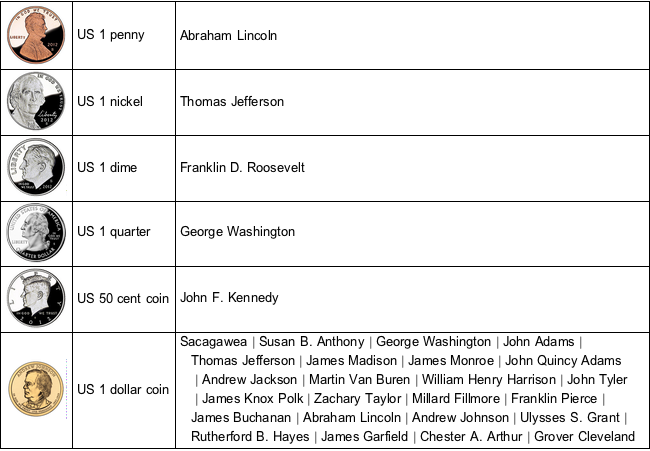
获取硬币面额（以美分计算）和质量（以克计算），并将质量转换为有理数.

In[5]:=

{values, masses} = 
 Transpose[EntityValue[coinsUS, {"Value", "Weight"}]]

Out[5]=

In[6]:=

coinsandweights = Transpose[{
   QuantityMagnitude[UnitConvert[values, "USCents"]],
   Rationalize[QuantityMagnitude[N[UnitConvert[masses, "Grams"]]]]
   }]

Out[6]=

In[7]:=

lcm = LCM @@ Denominator[Rationalize[coinsandweights][[All, 2]]];

In[8]:=

rationalcoinweights = lcm #2 & @@@ Rationalize[coinsandweights]

Out[8]=

找出与测量误差为 ± 0.1%（假设袋子本身可以忽略）的 1 磅重量测量相匹配的所有硬币分布.

In[9]:=

meanWeight = 
  QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]];

In[10]:=

error = Normal[Quantity[0.1, "Percent"]];

In[11]:=

{minScaledWeight, 
  maxScaledWeight} = {Floor[lcm meanWeight (1 - error/2)], 
  Ceiling[lcm meanWeight (1 + error/2)]}

Out[11]=

对于给定要求的总重量，用 FrobeniusSolve 决定所有可能的硬币组合.

显示完整的 Wolfram 语言输入

In[12]:=

allSolutions = Monitor[
   Table[fb = 
     FrobeniusSolve[rationalcoinweights, scaledweight], {scaledweight,
      minScaledWeight, maxScaledWeight}],
   Row[{NumberForm[
      100. (scaledweight - minScaledWeight)/(maxScaledWeight - 
          minScaledWeight), {4, 1}, "NumberPadding" -> {" ", "0"}], 
     "%: ", Length[fb], " solutions"}]
   ];

In[13]:=

Flatten[allSolutions, 1] // Length

Out[13]=

找出袋中硬币的总价值的最小值、中位数、均值和最高值（假设所有组合机会相同）.

显示完整的 Wolfram 语言输入

In[14]:=

coins = coinsandweights[[All, 1]];

In[15]:=

dollarValues = (coins.#/100.) & /@ Flatten[allSolutions, 1];

In[16]:=

TextGrid[With[{stats = {Min, Median, Mean, Max}}, 
   Transpose[{stats, 
     NumberForm[Quantity[#, "USDollars"], {\[Infinity], 2}] & /@ 
      Through[stats[dollarValues]]}]], Alignment -> {{Left, Decimal}},
   Dividers -> All, 
  Background -> {Automatic, {{LightBlue, None}}}] // TraditionalForm

Out[16]//TraditionalForm=

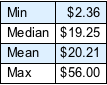
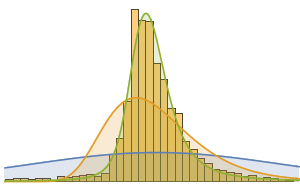
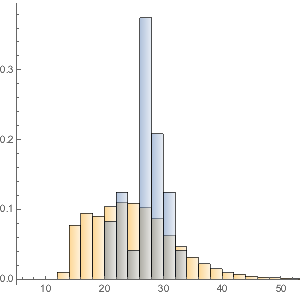
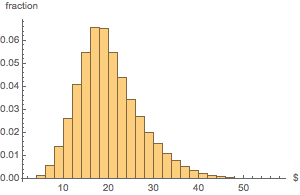
总货币价值分布的直方图.

In[17]:=

Histogram[dollarValues, Automatic, "PDF", 
 AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]

Out[17]=

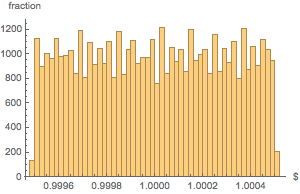
所有袋子的重量分布基本是均匀的.

显示完整的 Wolfram 语言输入

In[18]:=

weights = coinsandweights[[All, -1]];
lbg = QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]];
weightvalues = (weights.#)/lbg & /@ Flatten[allSolutions, 1];

In[19]:=

Histogram[weightvalues, 50, "PDF", 
 AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]

Out[19]=

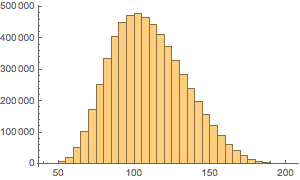
绘制硬币数量的分布图.

In[20]:=

Histogram[Total /@ Flatten[allSolutions, 1], {5}]

Out[20]=

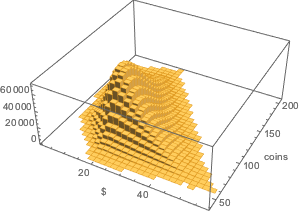
货币价值与袋中硬币数量的双变量分布.

In[21]:=

Histogram3D[{coins.#/100., Total[#]} & /@ Flatten[allSolutions, 1], 
 AxesLabel -> {Quantity[None, "USDollars"], "coins"}]

Out[21]=

Wolfram 语言™

估计一袋硬币的价值

相关范例