Mixed Quantities
Mixed quantities appear in multiple contexts: money, time, distance, weight, angles, etc.
In[1]:=
Quantity[MixedMagnitude[{2, 35, 21.2}],
MixedUnit[{"Hours", "Minutes", "Seconds"}]]Out[1]=
In[2]:=
UnitConvert[Quantity[75.562, "AngularDegrees"],
MixedUnit[{"AngularDegrees", "ArcMinutes", "ArcSeconds"}]]Out[2]=
In[3]:=
Quantity[MixedMagnitude[{5, 11}], MixedUnit[{"Feet", "Inches"}]]Out[3]=
In[4]:=
Quantity[MixedMagnitude[{5, 11}], MixedUnit[{"Feet", "Inches"}]];
% + Quantity[2.5, "Feet"]Out[4]=
The function SiderealTime returns a mixed quantity. Find the current sidereal time at your current location.
In[5]:=
stime = SiderealTime[]Out[5]=
Get the current position of the Sun in equatorial coordinates.
In[6]:=
sunpos = SunPosition[CelestialSystem -> "Equatorial"]Out[6]=
Compute the position of the Moon in the same coordinate system.
In[7]:=
moonpos = MoonPosition[CelestialSystem -> "Equatorial"]Out[7]=
Find the right ascension coordinate of the planets.
In[8]:=
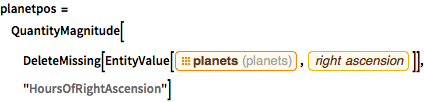
planetpos =
QuantityMagnitude[
DeleteMissing[
EntityValue[EntityClass["Planet", All],
EntityProperty["Planet", "RightAscension"]]],
"HoursOfRightAscension"]Out[8]=
Combine the various position measures into a list of right ascensions for each celestial body.
In[9]:=
ascensions = Join[ {0, moonpos[[1, 1]] - sunpos[[1, 1]]}, planetpos];show complete Wolfram Language input
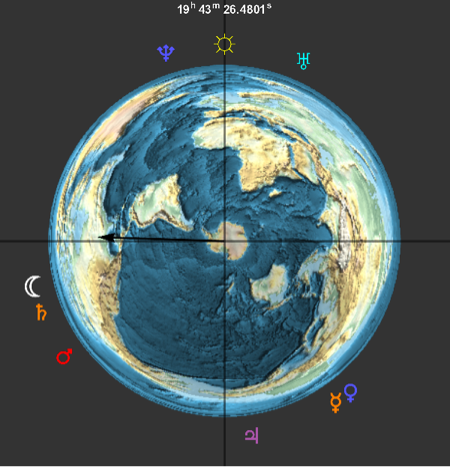
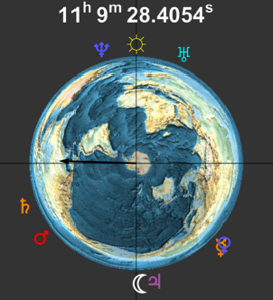
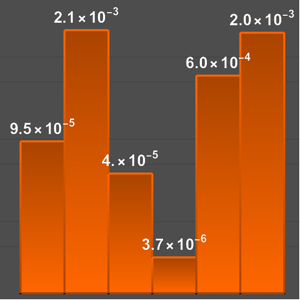
Create a graphic view of the location of the planets, Sun, and Moon as viewed from the South Pole.
show complete Wolfram Language input
Out[11]=