Gemischte Größen

Gemischte Größen treten in vielen Kontexten auf: Geld, Zeit, Distanz, Gewicht, Winkel etc.

In[1]:=

Quantity[MixedMagnitude[{2, 35, 21.2}], MixedUnit[{"Hours", "Minutes", "Seconds"}]]

Out[1]=

In[2]:=

UnitConvert[Quantity[75.562, "AngularDegrees"], MixedUnit[{"AngularDegrees", "ArcMinutes", "ArcSeconds"}]]

Out[2]=

In[3]:=

Quantity[MixedMagnitude[{5, 11}], MixedUnit[{"Feet", "Inches"}]]

Out[3]=

In[4]:=

Quantity[MixedMagnitude[{5, 11}], MixedUnit[{"Feet", "Inches"}]]; % + Quantity[2.5, "Feet"]

Out[4]=

Die Funktion SiderealTime gibt eine gemischte Größe zurück. Ermitteln Sie die aktuelle Sternzeit Ihres Standorts.

In[5]:=

stime = SiderealTime[]

Out[5]=

Ermitteln Sie den aktuellen Stand der Sonne in Äquatorialkoordinaten.

In[6]:=

sunpos = SunPosition[CelestialSystem -> "Equatorial"]

Out[6]=

Berechnen Sie den Stand des Mondes im selben Koordinatensystem.

In[7]:=

moonpos = MoonPosition[CelestialSystem -> "Equatorial"]

Out[7]=

Ermitteln Sie die Rektaszensionskoordinaten der Planeten.

In[8]:=

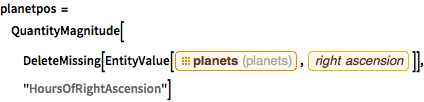
planetpos = QuantityMagnitude[ DeleteMissing[ EntityValue[EntityClass["Planet", All], EntityProperty["Planet", "RightAscension"]]], "HoursOfRightAscension"]

Out[8]=

Kombinieren Sie die unterschiedlichen Positionsmessungen zu einer Liste der Rektaszensionsdaten für jeden Himmelskörper.

In[9]:=

ascensions = Join[ {0, moonpos[[1, 1]] - sunpos[[1, 1]]}, planetpos];

In[10]:=

gp = Sequence[GeoRange -> "World", GeoProjection -> {"AzimuthalEquidistant", "Centering" -> {-90, 0}}]; globe = GeoGraphics[{Thick, Black, Arrow[{{0, 0}, $GeoLocation}]}, gp, GeoBackground -> GeoStyling["ReliefMap"]][[1, 1]]; cross = {Thickness[.005], Opacity[.5], Line[9.5 {-#, #}]} & /@ {{0, 1}, {1, 0}}; shade = GeoGraphics[{Opacity[.5], GeoDisk[{-sunpos[[2, 1]], 180}, 10018758]}, gp, GeoBackground -> None][[1, 1]];

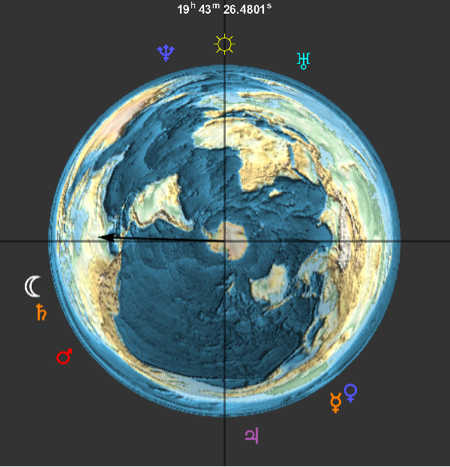
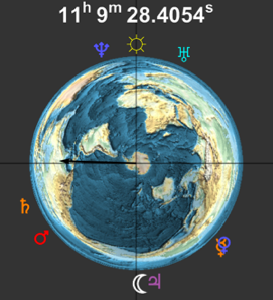
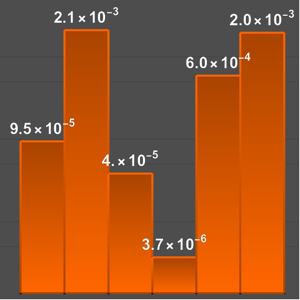
Erstellen Sie eine Graphik der Positionen der Planeten sowie von Sonne und Mond, so wie sie vom Südpol aus gesehen werden.

In[11]:=

Rasterize[ Graphics[{globe, cross, shade, MapThread[ Text[Style[#3, #2, 24, FontWeight -> Bold], {0, 3.5}.RotationMatrix[(#1) \[Pi]/12]] &, {ascensions, {Yellow, White, Orange, Lighter[Blue], Red, Lighter[Purple], Orange, Cyan, Lighter[Blue]}, {"☼", "\[Moon]", "\[Mercury]", "\[Venus]", "\[Mars]", "\[Jupiter]", "\[Saturn]", "♅", "\[Neptune]"}}]}, Background -> GrayLevel[0.2], PlotRange -> 4, PlotLabel -> #, LabelStyle -> {Bold, White}, Axes -> None] &@stime, RasterSize -> 600, ImageSize -> 450]

Out[11]=