The Equation of Time
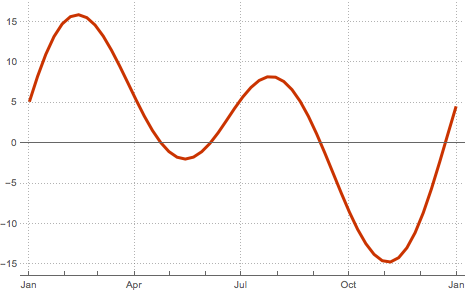
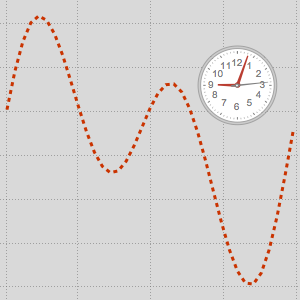
Due to the eccentricity of the Earth's orbit and the inclination of the Earth's axis with respect to the orbit's plane, the apparent motion of the Sun varies throughout the year. This induces a variation on time as measured by a sundial (apparent solar time) with respect to a more precise clock, for example, one determined by the apparent rotation of the fixed stars (sidereal time). This difference is known as the Equation of Time.
SiderealTime returns values of sidereal time as mixed-unit quantities, using MixedUnit.
SiderealTime[]SiderealTime[];
QuantityUnit[%]A sidereal time is actually an angle, and hence it can be converted into other angular units.
UnitConvert[SiderealTime[], "AngularDegrees"]The Equation of Time is determined by the motion of the Sun, as given by SunPosition. Compute weekly values at GMT noon.

dates = DateRange[
DateObject[{2015, 1, 1}, TimeObject[{12, 0}, TimeZone -> 0],
TimeZone -> 0.`],
DateObject[{2015, 12, 31}, TimeObject[{12, 0}, TimeZone -> 0],
TimeZone -> 0.`], 7];sunpos = SunPosition[GeoPosition[{0, 0}], dates,
CelestialSystem -> "Equatorial"]Use SiderealTime to compute the right ascension at the Greenwich meridian for the same weekly dates.
stime = SiderealTime[GeoPosition[{0, 0}], dates]Finally, find the corresponding values of the Equation of Time as the difference between the Sun's right ascension and the sidereal time at noon throughout the year. Express the result in minutes.
equationoftime =
UnitConvert[(TimeSeriesMap[First, sunpos] - stime),
"MinutesOfRightAscension"]Absolute values of the Equation of Time can be larger than 15 minutes.
MinMax[equationoftime]