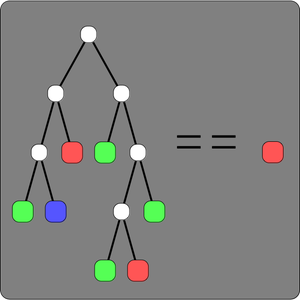
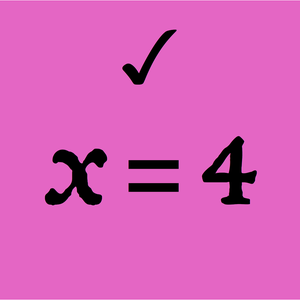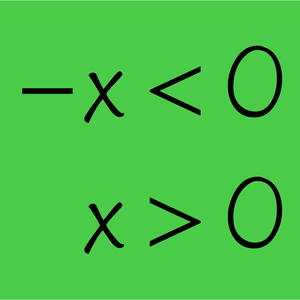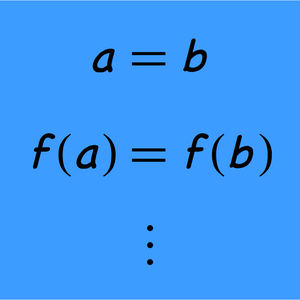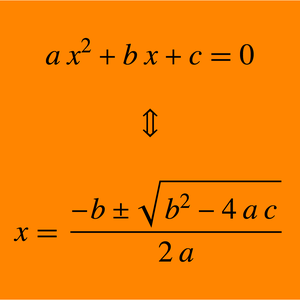布尔逻辑可能的最短的公理
可用单个运算符表示布尔逻辑的运算符,NAND 或 NOR。1913 年,Henry Sheffer 给出了三个公理,对它们的性质进行了完整的定义。2000 年,Stephen Wolfram 发现了单一算子的一个公理,可以证明 Sheffer 公理。Wolfram 还表明,这是可以构建布尔逻辑的最短公理。请到此博客查阅详细信息。
获取由 CenterDot 表示的运算符的三个 Sheffer 公理,用形式变量 a, b, c 表示任意命题。
这是 Wolfram 给出的布尔逻辑的最短公理。
函数 FindEquationalProof 可以根据 Wolfram 的公理构建 Sheffer 公理的证明。
也可以用 Sheffer 的公理来证明 Wolfram 的公理,说明两个公理系统是等价的。
还可以推出 NAND 的其他属性,如交换性。