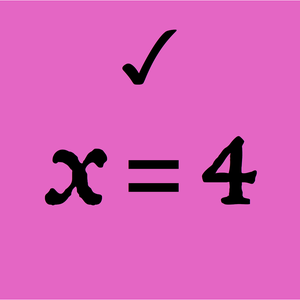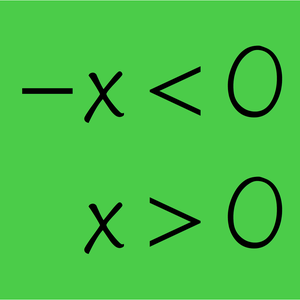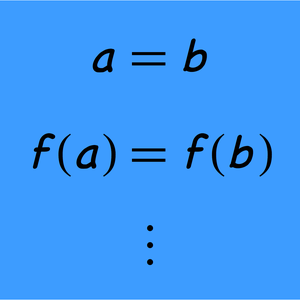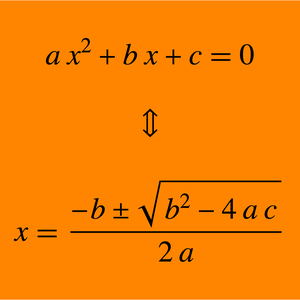ブール(Boole)論理についての最短の公理
ブール論理の演算子はNANDかNORの単独の演算子だけで表すことができる.1913年,Henry Shefferはこれらのいずれかの特性を完全に定義する3つの公理を提供した.2000年にStephen WolframはShefferの公理を証明することのできる,単独の演算子に対する単独の公理を発見した.Wolframはさらに,これこそがブール論理を構築することのできる最短の公理であることを示した.詳細はブログ記事でご覧いただきたい.
任意の命題を表す形式的な変数a,b,cを使って,CenterDotで表される演算子の3つのSheffer公理を取得する.
次はWolframが発見した,ブール論理についての最短の公理である.
関数FindEquationalProofは,Wolframの公理からShefferの公理の証明を構築することができる.
2つの公理システムの等価性を示すことによって,Shefferの公理からWolframの公理を証明することもできる.
可換性等,他のNANDの特性を導くこともできる.