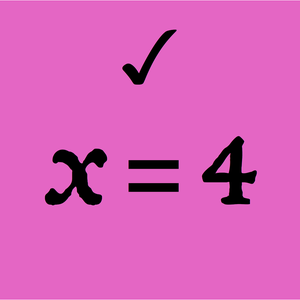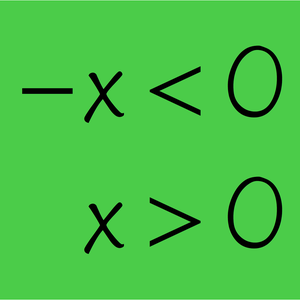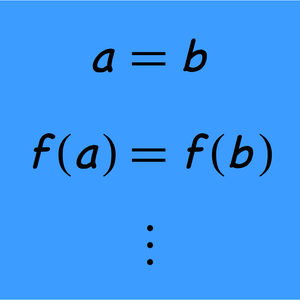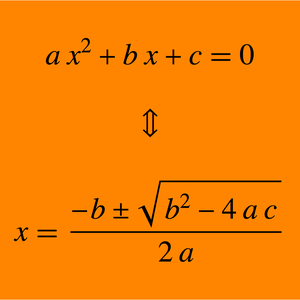The Shortest Possible Axiom for Boolean Logic

The operators of Boolean logic can be expressed in terms of just a single operator, either NAND or NOR. In 1913, Henry Sheffer gave three axioms fully defining the properties of either of those. In 2000, Stephen Wolfram found a single axiom for the single operator, from which Sheffer axioms can be proved. Wolfram also showed that this is the shortest possible axiom from which Boolean logic can be built. See this blog post for all the details.

Get the three Sheffer axioms for an operator represented by CenterDot, using formal variables a, b, c to stand for arbitrary propositions.

This is the shortest possible axiom for Boolean logic, as given by Wolfram.

The function FindEquationalProof can construct proofs of Sheffer's axioms from Wolfram's axiom.

It is also possible to prove Wolfram's axiom from Sheffer's axioms, demonstrating equivalence of the two axiom systems.

Other properties of NAND, like commutativity, can also be deduced.