Sprünge und Schnitte identifizieren
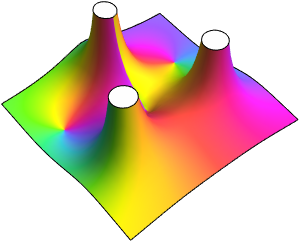
Diskontinuitäten in der Form von Sprüngen und Schnitten können Diagramme ergeben, die harte Farbübergänge aufweisen.
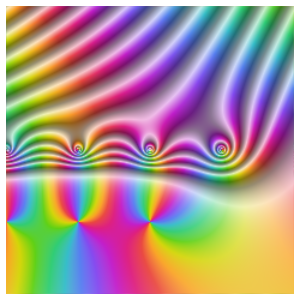
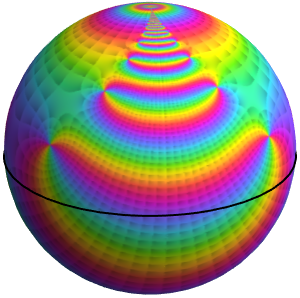
Der Schnitt einer Verzweigung von 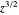 wird durch einen plötzlichen Sprung im Farbverlauf längs der Achse der negativen reellen Zahlen abgebildet. Das Farbenspektrum umkreist den Ursprung 1,5 Mal.
wird durch einen plötzlichen Sprung im Farbverlauf längs der Achse der negativen reellen Zahlen abgebildet. Das Farbenspektrum umkreist den Ursprung 1,5 Mal.
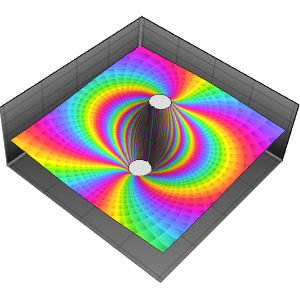
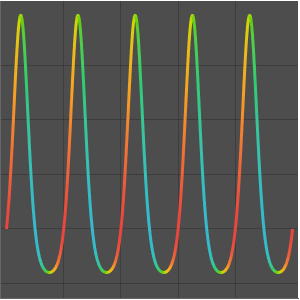
Eine Polstelle zeigt einen ähnlichen Sprung im Farbverlauf, da die Richtung von im Uhrzeigersinn zu gegen den Uhrzeigersinn wechselt.
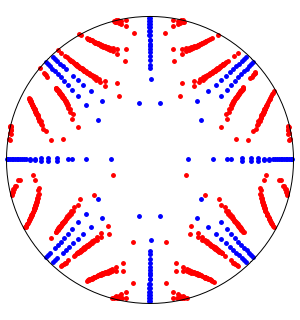
Should Floor[z] be linked?
Floor[z] ist innerhalb von Teilbereichen der komplexen Ebene konstant, weist jedoch krasse Sprünge zwischen den Regionen auf.