Eigenwerte von Graphen visualisieren
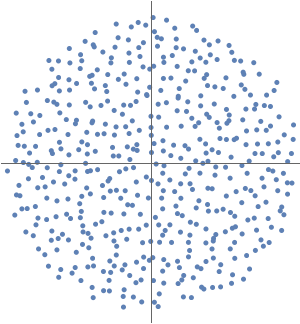
Eigenwerte von Graphen können Informationen über die strukturellen Eigenschaften des Graphen geben.
Generieren Sie aus einem Ausgangsgraphen einen gerichteten azyklischen Graphen.
Wenn ein Graph azyklisch ist, dann ist seine Adjazenzmatrix nilpotent und alle seine Eigenwerte sind Null.
Wenn ein Graph symmetrisch ist, dann ist seine Adjazenzmatrix symmetrisch und seine Eigenwerte sind reell.
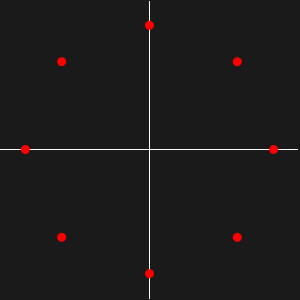
Wenn ein Graph bipartit ist, dann ist das Spektrum seiner Adjazenzmatrix rotationssymmetrisch in Bezug auf 0. Das heißt, wenn 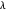 ein Eigenwert der Adjazenzmatrix ist, dann ist
ein Eigenwert der Adjazenzmatrix ist, dann ist 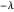 ebenfalls einer.
ebenfalls einer.
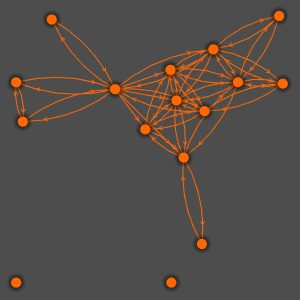
Generieren Sie einen Graphen, der einige Symbole veranschaulicht, die in der Wolfram-Dokumentation aufeinander verweisen.
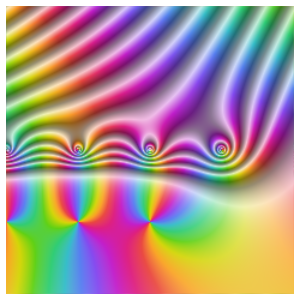
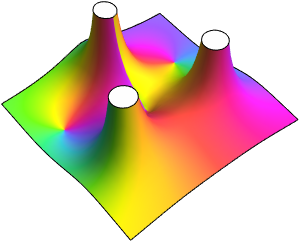
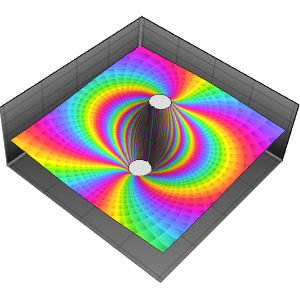
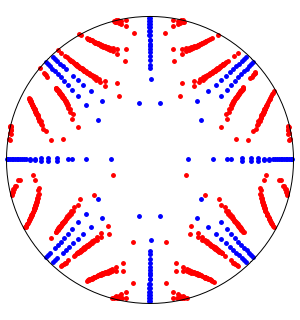
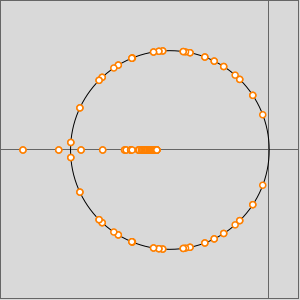
Durch die Visualisierung der Eigenwerte sieht man, dass Zyklen vorhanden sind, der Graph aber weder symmetrisch noch bipartit ist.
Der Graph ist nicht symmetrisch, weil ComplexExpand zu Complex, Conjugate, Im und Re hinweist und nicht umgekehrt.