Eigenwerte einer gedämpften Wellengleichung
Analysieren Sie die Stabilität von Lösungen einer partiellen Differenzialgleichung, indem Sie ihre Eigenwerte untersuchen. Alle Eigenwerte eines stabilen Systems haben negative Realteile.
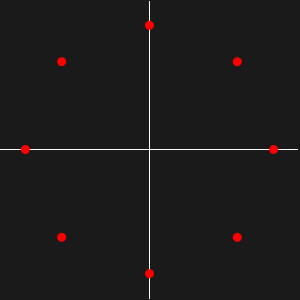
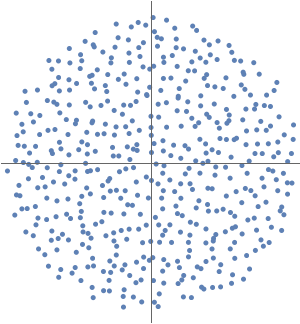
Berechnen Sie die ersten 100 Werte von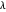 
und 
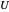, so dass 
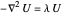auf der Einheitskreisscheibe und 
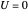auf dem Einheitskreis.
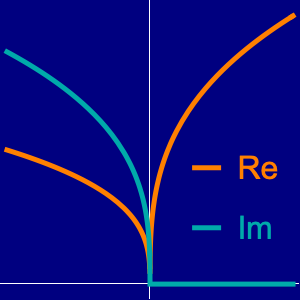
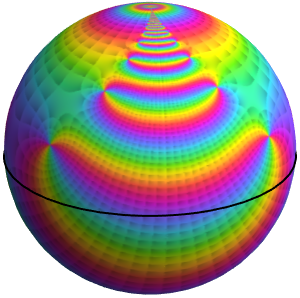
Verwenden Sie die vorigen Lösungen, um die strukturell gedämpfte Wellengleichung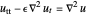 
mit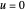 
auf der Einheitskreisscheibe zu lösen. Suchen Sie nach Lösungen der Form 
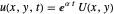. Kleinere Werte von 
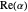entsprechen schnellerem Zerfall.
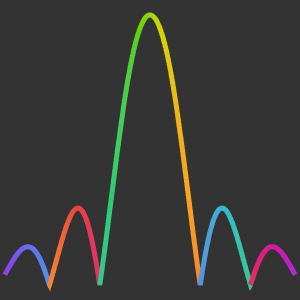
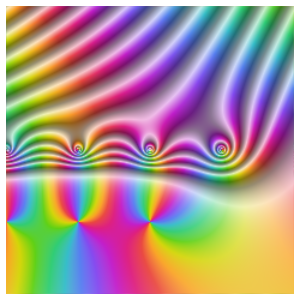
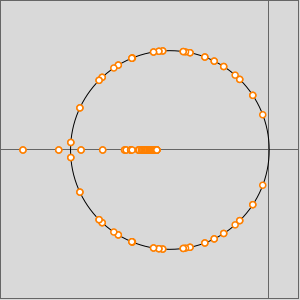
Visualisieren Sie den Effekt der dämpfenden Parameter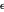 
auf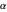 
. 
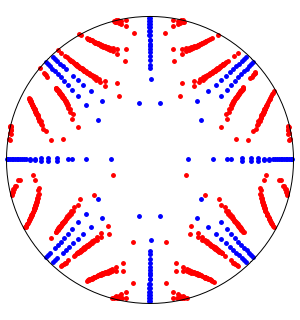
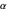-Werte akkumulieren sich bei 
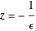und wenn 
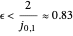, dann gibt es nicht-reelle Eigenwerte auf dem Kreis des Radius 
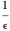mit Mittelpunkt 
.
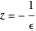Den kompletten Wolfram Language-Input zeigen
