Data Classification
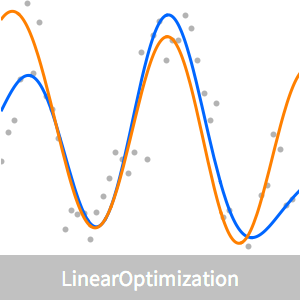
Find the minimum-degree polynomial that can separate two sets of points in the plane.
This example demonstrates how LinearOptimization may be used to test the feasibility (whether or not they can be satisfied) for a set of constraints. The constraints are generated symbolically from set data.
A polynomial 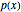 is said to separate two sets
is said to separate two sets 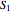 and
and 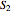 of points if
of points if 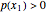 for all
for all 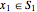 and
and 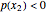 for all
for all 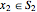 . Since there is no restriction on the size of the coefficients of
. Since there is no restriction on the size of the coefficients of 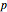 , the problem can be rescaled to require
, the problem can be rescaled to require 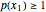 and
and 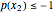 .
.
Define a polynomial power function that avoids issues with 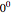 when
when 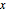 or
or 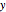 is 0.
is 0.
Define a function of 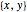 that is a polynomial of degree
that is a polynomial of degree 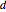 with coefficients
with coefficients 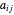 .
.
The variables for a degree 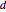 are the coefficients
are the coefficients 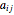 .
.
The constraints enforce separation between set 1 and set 2.
For example, here are the constraints for quadratics.
For separation, the only condition is that all the constraints must be satisfied. To find out if the constraints can be satisfied, the simplest thing is to set the objective vector to 0. Iteratively increase the polynomial degree till the constraints are satisfied.
Find the coefficients of the minimum-degree separating polynomial separating the two sets.
Visualize the separation of the sets using the polynomial.