Structure-Preserving Smoothing

Total variation fit regularization can be used to filter out noise in a signal while at the same time preserving jumps that are significant.

This example demonstrates how straightforward modeling in terms of Wolfram Language functions can be used to implement total variation fit regularization in a natural way using NArgMin.

For a signal 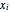, this is done by finding values 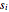that minimize 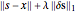, where 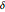s is the vector with elements 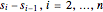and λ is a parameter that is used to trade off between noise reduction and proximity to the signal .

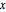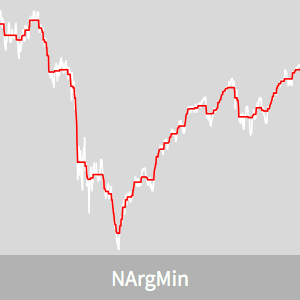
Consider the Dow Jones Industrial Average stock index during the 2008 financial crisis. There is a lot of day-to-day volatility that over a long term can effectively be considered noise.

The signal is the sequence of values of the stock index.

Find the smoothed index for 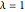. Method->"Convex" is used, since other methods would be very slow if they succeeded at all for this many variables.

Compare the smoothed index with the actual index.

The smoothed index shows the main trends but misses some important features. There is a trade off between catching features and how much smoothing is done that is determined by 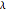. For 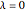, there is no smoothing and 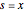. On the other hand, as 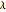approaches ∞, 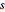will approach a constant signal. A plot of the total variation versus the deviation from the original signal for different values of 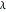can give an indication of appropriate values of 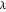to achieve the best balance.

There is a noticeable bend in the curve around 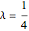, indicating that this achieves a reasonable balance.

It is interesting to look at the smoothed index for some of the different values of .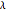

The minimization can also be thought of in terms of doing a least squares fit with regularization. The new FitRegularization option may be used in Fit to do this.