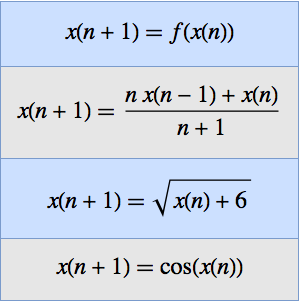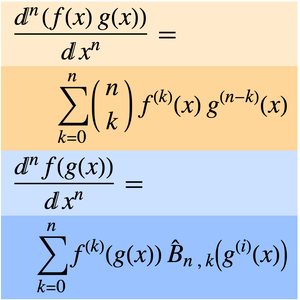楕円曲線についてクライン(Klein)の不変量を計算する
ワイエルシュトラス(Weierstrass)の楕円曲線の不変量は,楕円曲線に対して定義される標準的な概念である.バージョン12は,これらの不変量の他,これらの楕円関数の半周期および半周期の値を直接扱うための関数を提供する.
WeierstrassE1,WeierstrassE2,WeierstrassE3は対応する半周期におけるWeierstrassPの値を与える.
同様にWeierstrassEta1, WeierstrassEta2,WeierstrassEta3は対応する半周期におけるWeierstrassZetaの値を与える.
WeierstrassInvariantG2とWeierstrassInvariantG3はワイエルシュトラスの楕円関数の不変量を定義する.これによって以下のような例で不変量を使うことが簡単になる.
ワイエルシュトラスの楕円関数の判別式を定義する.
曲線のg不変量を使って,クラインのj不変量を計算する.
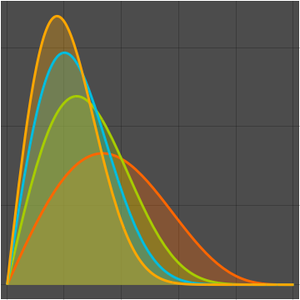
クラインの不変量の虚部をプロットする.
完全なWolfram言語入力を表示する
組込み関数の値と比較する.