j-Invariante für eine elliptische Kurve berechnen
Invarianten sind ein wichtiges Konzept auf dem Gebiet der elliptischen Kurven. Version 12 bietet Funktionen, die sowohl das direkte Arbeiten mit diesen Invarianten als auch Berechnungen und Operationen mit Halbperioden und den Werten von Halbperioden von elliptischen Funktionen ermöglichen.
WeierstrassE1, WeierstrassE2 und WeierstrassE3 liefern die Werte von WeierstrassP der jeweiligen Halbperiode.
Ganz ähnlich liefern WeierstrassEta1, WeierstrassEta2 und WeierstrassEta3 die Werte von WeierstrassZeta der jeweiligen Halbperioden.
WeierstrassInvariantG2 und WeierstrassInvariantG3 definieren die Invarianten für die Weierstraßschen Funktionen, was in den folgenden Beispielen praktisch ist.
Definieren Sie die Diskriminante der Weierstraßschen Kurve.
Berechnen Sie die j-Invariante anhand der g-Invarianten der Kurve.
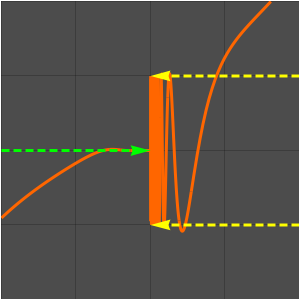
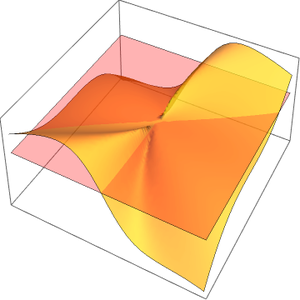
Plotten Sie den Imaginärteil der j-Invariante.
Vergleichen Sie dies mit dem Wert, den die eingebaute Funktion zurückgibt.