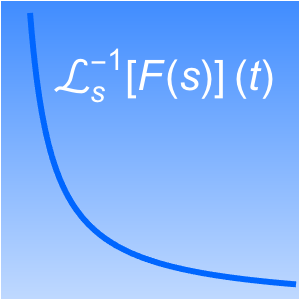
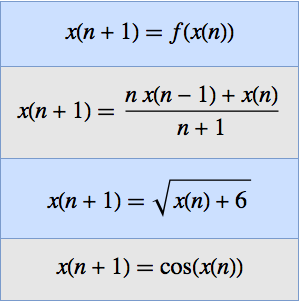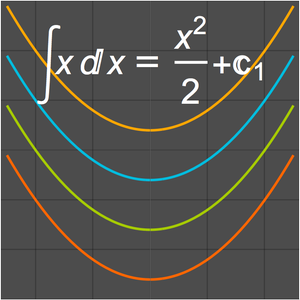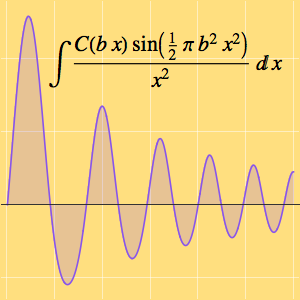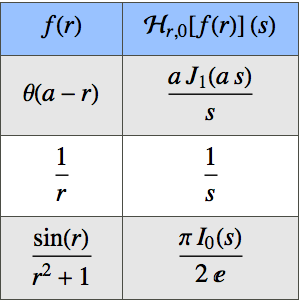Find the Limit of a Sequence
Limits of sequences arise frequently in calculus, and may exist even if the corresponding function limits do not exist. The DiscreteLimit function in Version 12 can be used to compute the limits of sequences given in closed form or specified by formal operators, as illustrated by the following examples.
Find the limit of a sequence.
Visualize the sequence.
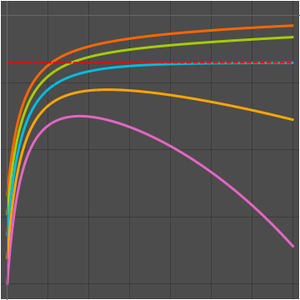
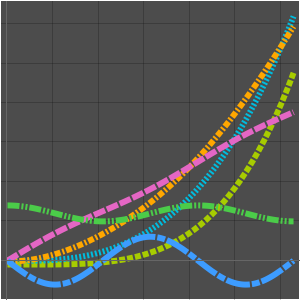
Find the limit of a multivariate sequence.
Visualize the sequence.
The following example uses the Stolz–Cesàro rule, a discrete version of L'Hôpital's rule for limits, to compute the limit of a nested Inactive sum.
Find the limit of an Inactive continued fraction.
The following example demonstrates that a function limit may not exist, but the corresponding sequence limit does exist.
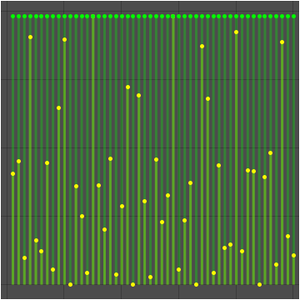
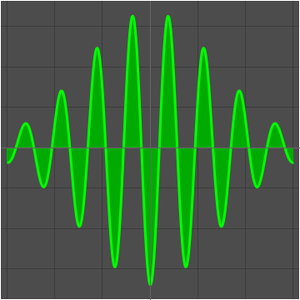
Define a trigonometric function.
Plot the function and the sequence obtained by sampling the function at integers.
Here, the function limit does not exist.
This is because the function values oscillate between -1 and 1.
However, the sequence limit does exist.
This is because the sequence is constant at all the sample points.