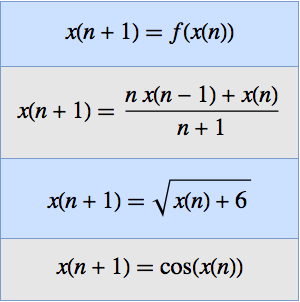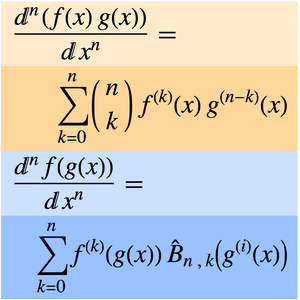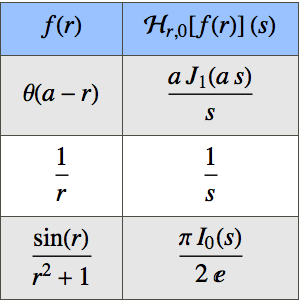Invert a Laplace Transform Using Post's Formula
Emil Post (1930) derived a formula for inverting Laplace transforms that relies on computing derivatives of symbolic order and sequence limits. Here, Post's inversion formula is implemented using the new capabilities of D and DiscreteLimit.
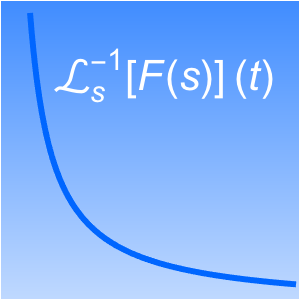
Post's inversion formula may be stated as follows.
Define a function that implements Post's inversion formula.
Compute the inverse Laplace transform of 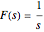 using the formula.
using the formula.
Obtain the same result using InverseLaplaceTransform.
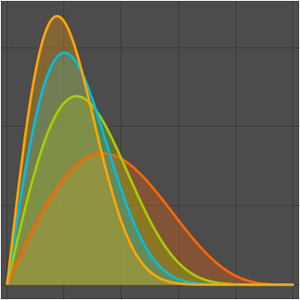
Create a table of basic inverse Laplace transforms using Post's inversion formula.
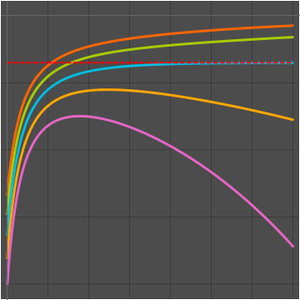
The Post formula can also be used for the numerical approximation of inverse Laplace transforms by using derivatives of sufficiently high order, as illustrated in the following.