计算晶格的排列密度
"Lattice" 实体域包含经典的已命名晶格的有用信息。
例如，考虑体心立方 (BCC) 晶格，可使用 "Image" 属性立即显示。
晶格排列的一个重要特性是按相关构型进行填充的球体占据的空间比例。下面给出了 BCC 晶格的排列密度。
换句话说，体心立方排列方式中，球体占据了约 68％ 的总空间。
通过 "MinimalVectors" 属性可获取生成这些晶格的最小向量。
根据这些结果，可以进行空间填充可视化，从中可以直接计算密度。首先构建一个列表，给出根据最小向量出现在单位晶格中的球体的中心。
现在将绘图范围限制为单位晶格大小的区域。
通过使用填充球而不是空心球可以使可视化更具体。
从该图中可以看出，单位晶格中有八个八分之一球和一个完整的球，总共是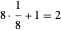 
个完整的球。以 
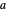作为球体的半径，通过对空间对角线应用毕达哥拉斯定理，得出整个立方体的边长为 
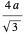，意味着球体的堆积密度由我们已经上面看到的表达式给出。
现在考虑面心立方 (FCC) 晶格。
这种晶格排列的密度较高。
即在面心立方排列方式中，球体占据了约 74% 的总空间。
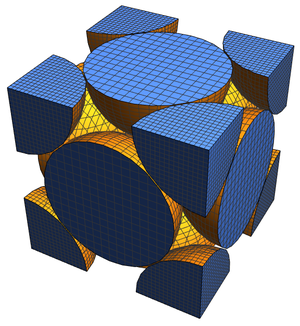
和以前一样，首先找到 FCC 排列方式中球体的中心，进行空间填充可视化。
从该图中可以看出，单位晶格中有八个八分之一球和六个半球，总共是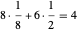 
个完整的球。以 
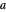作为球体的半径，通过对空间对角线应用毕达哥拉斯定理，得出整个立方体的边长为 
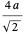，意味着球体的堆积密度由我们已经获得的表达式给出。
六方最密堆积 (HCP) 是另一种密切相关的排列方式。
它与面心立方的排列密度一样。
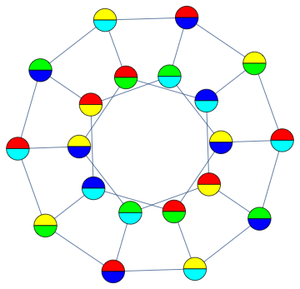
如在面心立方密积中一样，每个球体被 HCP 中的 12 个其他球体包围。取这种排列的最小向量的 Delaunay 网格相当于将外面的 12 个球体的中心连在一起，并将边变作包围多面体 (enclosing polyhedron) 的面。
所得的多面体被称为同相双三角台塔 (triangular orthobicupola)。
