研究函数空间
函数空间是从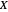集合 
到集合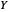 
的一组给定类型的函数。它被称为空间，是因为在许多应用中它是拓扑空间并且通常与测度空间相关联。
函数空间往往涉及非常广义和抽象的拓扑概念。"FunctionSpace" 实体域涵盖了超过 125 个空间的属性，并尽可能以计算的形式提供给用户。
例如，Lebesgue 空间的定义是有限维向量空间的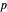 
-norm 的自然推广。可通过 Wolfram|Alpha 查询直接获取 
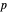阶 Lebesgue 空间在 
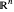上的属性总结，这里只显示最重要的几个单元。
实际上根据它们的域和测度空间，定义了许多 Lebesgue 空间。
现在考虑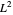 
空间的特殊情况，其范数定义如下。
这里，PureMath 部分被用作尚未整合到 Wolfram 语言中的数学对象的占位符。
还可获取研究每个空间的知名人士的信息。
为方便起见，还提供了一个表格，显示了每个空间使用的各种符号。
现在进行一些简单的计算，说明如何使用该实体域中的信息。
考虑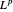 
的对偶空间 (
)。
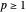现在取对偶空间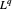 
的对偶，并对所得参数化实体进行符号简化。
这实际上等于原来的空间，可以看出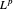 
是自反的，即 
。
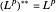也可以直接进行计算。
可通过 "TypesetDescription" 属性获取更多详细信息，对于自反空间，给出了以下严格的定义，以及其他一些有用的说明。
