图的分数着色
利用图论工具可以描述和解决许多涉及网页排名、电子电路设计、社交网络分析和分布管理等不同领域的现代问题。除了用于构建、计算和对图进行操作的大量函数之外，Wolfram 语言还包括许多图的集合。
"Graph" 实体域试图对有趣的无向图及其已知或可计算的许多属性进行归类。"Graph" 实体提供了超过 6,000 个简单图和 500 个预先计算的属性，并且还在持续增加中。
"Graph" 实体框架还包括预先计算的 "nice" 嵌入。
注意 "Graph" 属性返回的对象不是简单的图，而是 Wolfram 语言 Graph 对象。
每个图实体都包含它所属的数学类别的详细列表。
还有两个函数将图实体的世界与顶层图对象连接起来。ToEntity 将未知简单图转换为实体（如果存在的话） 。
转换由 FromEntity （相当于使用 "Graph"属性） 提供。
下面来说明 "Graph" 实体域中可用数据的广度，请考虑图的所谓分数色数 (fractional chromatic number)。分数色数将通常的色数推广为着色的情况，其中，在每个顶点处允许使用多种颜色，每种颜色具有指定的权重分数，使得相邻的顶点不包含两种一样的颜色。
例如，虽然十二面体图的色数为 3（需要最少三种颜色来为顶点着色，才能使得没有两个相邻顶点共享一种颜色），但使用分数着色会得到一个分数色数 5/2（其中一个实例，将在后面进行讨论，由分配给每个节点的五种颜色组成，每种颜色的权重为 1/2）。
图实体域包含许多图的常用色数和分数色数，以及实现这些最小值的具体着色方法。例如，十二面体图的色数为 3。
可用以下方式获取实现该色数的着色方案。
使用此嵌入和着色数据以及内置的用于图操作的功能来进行可视化是很简单的事儿。
可以通过观察（或编程）验证，上图中没有两个相邻的顶点共享相同的颜色。
分数着色的情况稍微复杂一些，允许顶点上不同颜色的权重为分数，放宽了每个顶点具有唯一颜色的约束。然后对所有顶点上的分数求和来定义分数色数。这样通常允许使用“更少”（但不一定是整数）的颜色来进行着色。例如，十二面体图的分数色数是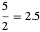 
，小于它的色数 3。
使用 "MinimumWeightFractionalColoring" 属性获取顶点列表及不同颜色的权重。
例如，上面的输出表明使用五种颜色即可实现最小的分数着色，第一种颜色应用于顶点 3、5、9、12、13、15、16、20，权重为 1/2，依此类推。由于每种颜色的权重均为 1/2，因此总的分数色数为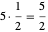 
。
因为这种情况下每个着色的分数等于 1/2，所以通过找到对每个顶点有贡献的两种颜色可以很容易地进行可视化。
例如，上面的列表表明第一个顶点使用颜色 4 和 5，第二个顶点也使用颜色 4 和 5，第三个使用颜色 1 和 5，依此类推。现在将颜色索引转换为实际颜色。
可视化的最后一步是定义一个由两个颜色适当的半圆盘组成的顶点形状函数。
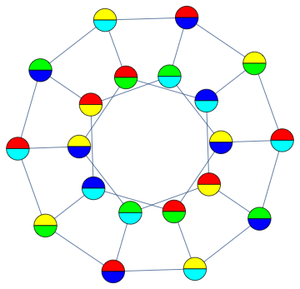
准备妥当，现在可以显示十二面体图的最小分数着色。
不出所料，相邻顶点在此分数着色中没有共享相同的颜色。
分数色数不是均匀分布的，而是倾向于汇聚在某些值周围。使用 "Graph" 实体域中为所有图预先计算的数据绘制直方图，显示了在整数周围汇聚的情况，也有一些峰值出现在其他地方。
可以用 BubbleChart 绘制具有每个分数色数的图的数量（分子位于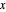 
轴上，分母位于 
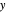轴上），进而对分布进行更细致的研究。
