形状给定情况下最有效的容器
"Solid" 实体域包含具有数学意义的封闭立体区域。
每个立体都有许多属性。
当然,其中包括表面积和体积。
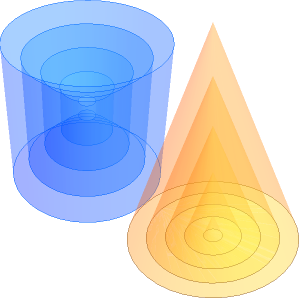
众所周知,填充球体(球)的表面积与体积之比是所有形状中最小的。然而,对于其他立体形状,研究一下与最小化包围一定体积所需的表面积对应的周长也很有趣。例如,很容易证明包围体积最有效的圆柱体是高度与底的半径比 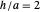 (或者说底的直径等于高)的圆柱体.
(或者说底的直径等于高)的圆柱体.
还可以考虑其他立体形状,为简单起见,将体积定为 1。
对于所有的长方体,立方体(即等边长方体)给出每单位表面积最大的体积。
沿直角坐标轴的边长相等时,包围的体积一定的情况下,直角四面体的表面积最小。
对于圆锥体,可以用解析式算出给出最小表面积的尺寸。
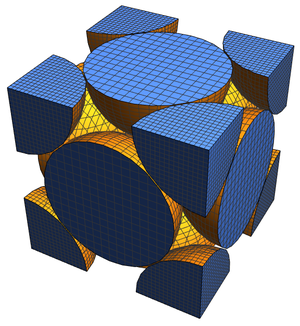
现在,可视化随着整体尺寸的变化最有效的那个形状。