Wolfram Language™

Investigue a hipótese de Riemann

Publicado pela primeira vez em um artigo inovador em 1859 por Bernhard Riemann, a hipótese de Riemann é uma conjectura matemática profunda que declara que os zeros não-triviais da função zeta de Riemann, ou seja, os valores da função zeta de Riemann

exceto 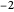, , 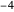, 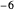… tal que 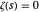pertencem todos à "linha crítica" 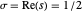, onde 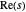denota a parte real de uma variável complexa .

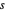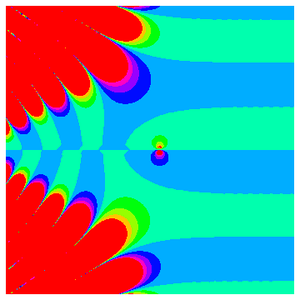
Enquanto a função zeta de Riemann oscila infinitamente ao longo do eixo real negativo, ela se aproxima assintoticamente de 1 ao longo do eixo real positivo.

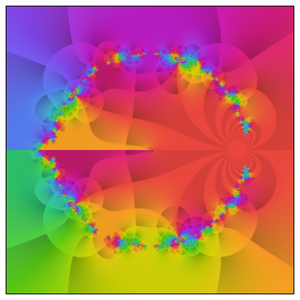
O comportamento fica ainda mais complicado ao longo da linha crítica.

De fato, o gráfico anterior fornece uma idéia mais representativa da verdadeira complexidade que surge no plano complexo.

Os 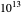primeiros zeros não triviais da função zeta de Riemann foram testados e encontrados para satisfazer a hipótese de Riemann. Portanto, é bastante surpreendente que, apesar de tantas evidências numéricas e de esforços consideráveis, ninguém tenha sido capaz de provar a hipótese nos últimos 160 anos.

Muitos resultados em matemática são conhecidos "assumindo que a hipótese de Riemann seja válida". Isso significa que uma prova da hipótese de Riemann estabeleceria imediatamente uma infinidade de outros resultados em matemática. Também existem muitas formulações alternativas da hipótese de Riemann, uma coleção que o domínio da entidade RiemannHypothesisFormulation tenta coletar.

Atualmente, a coleção contém um total de aproximadamente 70 formulações.

Essas formulações, por sua vez, podem ser agrupadas em cerca de metade do número de famílias.

A forma original da hipótese de Riemann pode ser declarada usando a aritmética do quantificador na seguinte forma concisa.

Embora, em princípio, essa seja uma expressão calculável, já que ninguém sabe como estabelecer a hipótese de Riemann, a aplicação de um quantificador à hipótese retorna "não calculado" (afinal, se o Mathematica pudesse resolver os quantificadores nesse caso, seria capaz de estabelecer a validade de a hipótese de Riemann).

Agora examine os tipos de formulações alternativas presentes no domínio RiemannHypothesisFormulation.

Talvez a afirmação alternativa mais famosa da hipótese de Riemann diz respeito à positividade de expressões dadas por derivadas da função 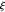—uma função intimamente relacionada à 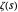—é a desigualdade de Li. Essa formulação, conhecida como desigualdade de Li, pode ser formalmente declarada da seguinte forma.

A Wolfram Language pode calcular diretamente formas fechadas para a expressão dentro da desigualdade (embora fazer isso para grandes índices exija o uso de relações de recorrência conhecidas que são satisfeitas pelas derivadas de 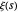). Para começar, primeiro extraia a desigualdade da formulação.

Agora defina as constantes de Li 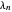cuja positividade para todos os 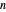positivos é equivalente à hipótese de Riemann.

Calcular exatamente e numerar as constantes até a ordem cinco verifica se elas são realmente positivas.

Obviamente, a desigualdade de Li é apenas uma formulação alternativa. Vários matemáticos derivaram múltiplas formulações para a hipótese de Riemann. Aqui está uma lista de formuladores ordenados pelo número de formulações distintas representadas na coleção.

Agora você pode criar uma linha do tempo de matemáticos que estudaram a hipótese de Riemann para ilustrar alto nível de atividade dedicada à bela, porém complexa, hipótese de Riemann.