研究黎曼猜想
Bernhard Riemann 于 1859 年在一篇开创性论文中首次发表黎曼猜想，这是一个深刻的数学猜想，它表明黎曼 zeta 函数的非平凡零点，即黎曼 zeta 函数的值
除去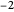 
、
、
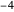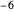、…，满足 
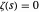的点都位于“临界线” 
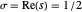上，其中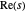 
表示复变量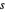 
的实部。
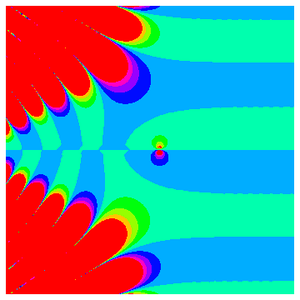
尽管黎曼 zeta 函数沿负实轴无限振荡，沿正实轴则渐近接近于 1。
临界线上的行为变得更加复杂。
事实上，前面的图给出了复平面上真实复杂性的更具代表性的图景。
黎曼 zeta 函数的前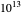 
个非平凡零点已被测试过，它们全部满足黎曼猜想。因此，相当令人惊讶的是，尽管有如此丰富的数值证据，而且人们也付出了巨大的努力，但在过去的 250 年中，没有人能够证明这一猜想。
许多数学结果“以黎曼猜想的成立为前提”。这意味着如果黎曼猜想被证明，则其他大批数学结果也立即成立。还可用其他方式陈述黎曼猜想，这正是 RiemannHypothesisFormulation 实体域试图收集的集合。
该集合目前大约有 70 种不同的陈述方式。
这些陈述方式又可以被大致归为 35 个类别。
可以通过 quantifier arithmetic 以下面的简洁形式陈述原始形式的黎曼猜想。
原则上说，这是一个可计算的表达式，但由于没有人知道如何建立黎曼猜想，消除 quantifier 是无法计算的（毕竟，如果 Mathematica 能够在这种情况下解出 quantifier，它将能够确定黎曼猜想的有效性。）
现在来查看 RiemannHypothesisFormulation 实体域中出现的其他陈述方式。
黎曼猜想可能最有名的替代陈述是 Li 不等式，即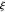 
-函数（与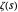 
密切相关的一个函数）的导数表达式的正性。可用以下式子表示该陈述方式，即 Li 不等式。
Wolfram 语言可直接对不等式内的表达式的解析形式进行计算（尽管对较大的索引这样做需要使用已知的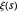 
的导数满足的递归关系）。首先从式子中提取不等式。
现在定义 Li 常量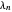 
，它对所有正 
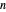的正性等价于黎曼猜想。
进行精确计算并将常量数值化到五阶，证明它们确实是正的。
当然， Li 不等式只是一个替代的表述。许多数学家已经得出了黎曼猜想的多种陈述方式。以下是按集合中不同陈述方式的数量排序的数学家的列表。
现在来构建一个研究人员时间表，这个时间表在某种程度上说明了人类为研究黎曼美秒而顽固的猜想付出了多少努力。
