Wolfram 언어™

리만 가설 조사하기

1859년 획기적인 논문에서 처음 발표된 베른하르트 리만(Bernhard Riemann)의 가설은, 비수용적인 리만 제타 함수의 영점, 즉 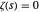인 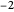, , 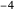, 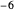… 이외의 리만 제타 함수의 값은

모두 "임계선" 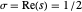에 위치하며, 여기서 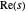은 복소 변수 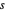의 실제 부분을 나타냅니다.

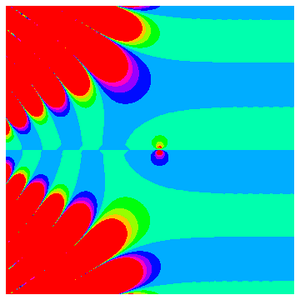
리만 제타 함수는 음의 실수 축에 따라서 무한으로 진동하는 한편, 이는 양의 실수 축에 따라 점근적으로 1에 다가옵니다.

이 동작은 임계선을 따라 더욱 복잡해집니다.

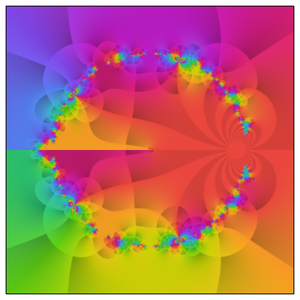
앞부분의 플롯은 사실 복소 평면에서 발생하는 진정한 복잡성을 잘 나타내고 있습니다.

리만 제타 함수의 첫 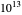개의 비자명한 영점은 검정되어 리만 가설을 만족하는 것으로 알려졌 있습니다. 그러므로 이러한 충분한 수치적 증거와 상당한 노력이 이루어지고 있음에도 불구하고 지난 250년 동안 아무도 이 가설을 증명할 수 없었다는 것은 다소 놀랍습니다.

수학 결과의 대부분은 "리만 가설이 참이라고 가정할 때"라고 되어 있습니다. 즉, 리만 가설이 증명됨으로써, 그 외의 다수의 결과도 즉시 확립한다는 것을 의미합니다. 리만 가설을 대체할 공식 역시 존재하며 RiemannHypothesisFormulation 실체 영역은 이러한 리만 가설의 대체 공식을 수집하는 시도를 하고 있습니다.

현재 이 컬렉션에는 대략 70의 공식화가 포함되어 있습니다.

이러한 식은 그 반의 족으로 그룹화할 수 있습니다.

원래의 리만 가설 형식은 다음의 간단한 형식으로 한정 기호를 사용한 연산으로 나타낼 수 있습니다.

이것은 원리상으로는 계산 가능하지만, 아무도 리만 가설을 구축하는 방법을 모르기 때문에 그것에 한정 기호 소거를 적용하면 평가할 수 없게 되어 버립니다(만약 Mathematica가 이 경우에 한정 기호를 풀 수 있다면, 리만 가설의 타당성을 증명할 수 있을 것입니다).

RiemannHypothesisFormulation 영역에 존재하는 다른 식의 유형을 조사합니다.

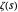와 깊이 관련된 함수인 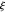함수의 도함수에 의해 주어지는 식의 양수값에 관한 리만 가설의 가장 유명한 대체 문장은 아마도 Li의 부등식일 것입니다. Li의 부등식으로 알려진 이 식은 다음과 같은 공식으로 말할 수 있습니다.

Wolfram 언어는 부등식 내부의 식에 대한 닫힘 형식을 직접 계산할 수 있습니다.(대규모 지표로 계산하면 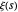의 도함수에 의해 만족되는 기존의 재귀 관계 사용이 필요하게 됩니다.) 우선 식에서 부등식을 추출합니다.

Li의 상수 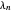을 정의합니다. 모든 양의 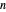에 대한 이 상수의 정의 값은 리만 가설과 같습니다.

엄밀하게 계산하고 상수를 5차까지 수치화하면 그것이 실제로 양수임이 증명됩니다.

물론 Li의 부등식은 하나의 대체식에 불과합니다. 다수의 수학자가 리만 가설에 대해서 다양한 공식을 내놓았습니다. 다음은, 컬렉션 중의 다른 공식화의 수에 의해 정렬된 공식의 명단입니다.

이것으로 아름답지만 고집스럽게 풀리지 않는 리만의 가설에 투입된 높은 수준의 활동을 어느 정도 보여주는 수학자의 타임 라인을 구축할 수 있습니다.