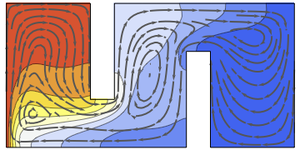
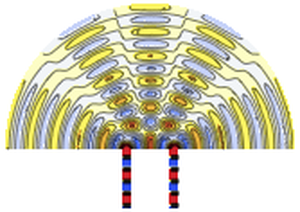
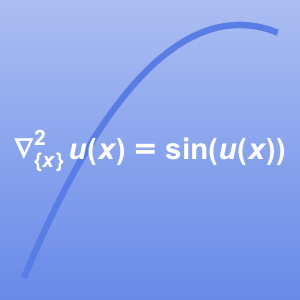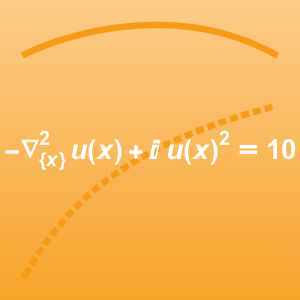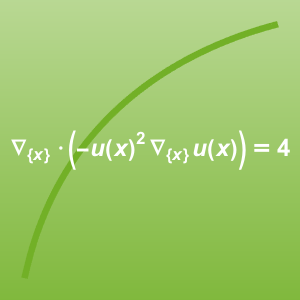Transporte de energía
Resuelva un problema de multifísica que une la ecuación de Navier–Stokes con una ecuación del calor:
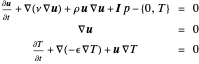
Aquí,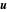 
es el campo de velocidades valuado vectorialmente, 
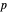es la presión e 
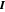es la matriz de identidad. 
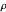y 
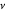son la densidad y viscosidad dinámica respectivamente. 
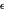es la capacidad térmica del líquido, y 
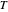es la temperatura.
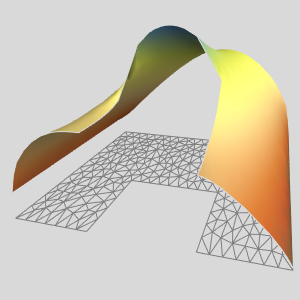
Especifique los parámetros, y una región rectangular con recortes.
Visualice la región.
Especifique un número de Prandtl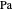 
y un número de Rayleigh 
.
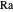Establezca una ecuación viscosa de Navier–Stokes acoplada a una ecuación del calor utilizando una aproximación de Boussinesq. Use los parámetros de material especificados.
Establezca condiciones de frontera sin deslizamiento para las velocidades en todas las paredes de frontera.
Establezca un punto de presión de referencia.
Especifique una diferencia de temperatura entre las paredes izquierda y derecha.
Reemplace los parámetros en las condiciones de frontera.
Establezca las condiciones iniciales de manera que el sistema se encuentre en reposo.
Siga el progreso de integración temporal y el tiempo total que tome resolver la ecuación diferencial parcial utilizando un espacio de malla especificado, e interpolando las velocidades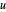 
y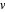 
, y la temperatura 
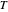con segundo orden y la presión 
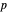con primer orden.
Cree una visualización de la frontera de la región.
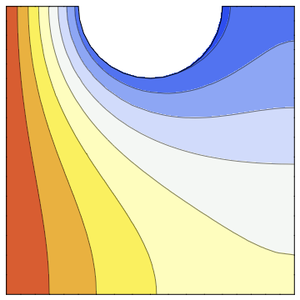
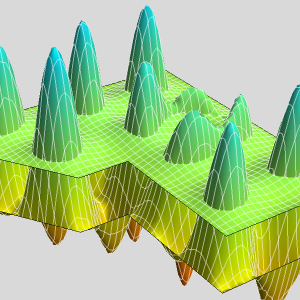
Visualice la distribución de presión.
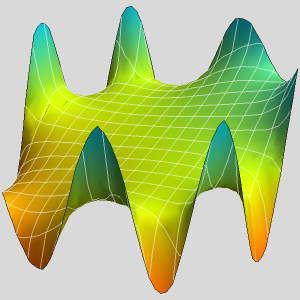
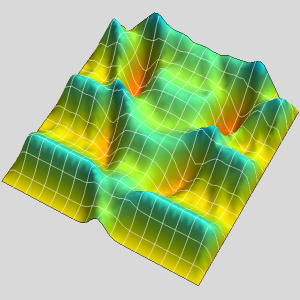
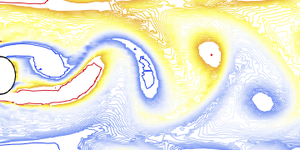
Visualice la distribución de temperatura.
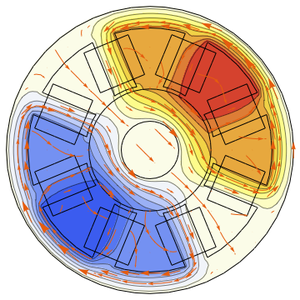
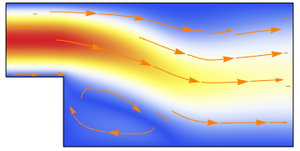
Visualice el campo de velocidades.
Cree una animación del cambio de temperatura y las líneas de corriente de velocidad.
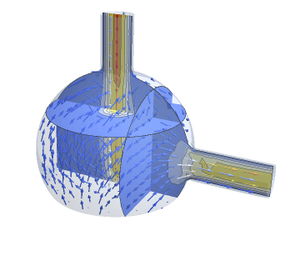
Los curiosos pueden investigar el campo de velocidades diferente que se produce al cambiar la posición de los recortes.
