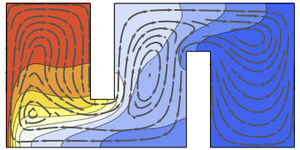
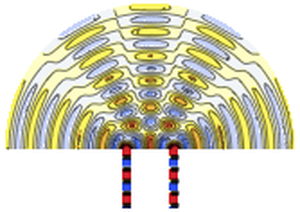
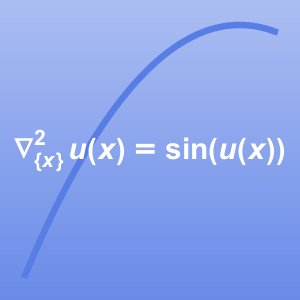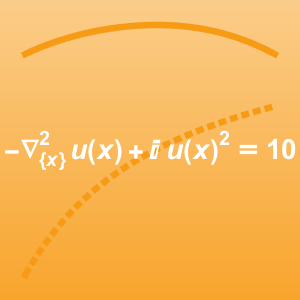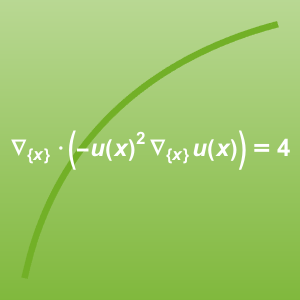Transport d'énergie
Résolvez un problème multi-physique qui associe l'équation de Navier-Stokes à une équation de chaleur :
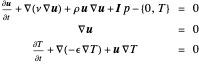
Ici, 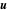 correspond au champ de vélocité à valeurs vectorielles en trois dimensions,
correspond au champ de vélocité à valeurs vectorielles en trois dimensions, 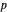 représente la pression et
représente la pression et 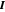 la matrice d'identité.
la matrice d'identité. 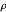 et
et 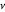 sont respectivement la densité et la viscosité dynamique.
sont respectivement la densité et la viscosité dynamique. 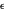 correspond à la capacité calorifique du liquide et
correspond à la capacité calorifique du liquide et 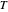 à la température.
à la température.
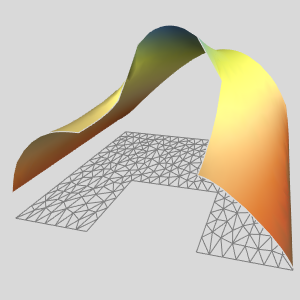
Spécifiez les paramètres et une région rectangulaire avec des découpes.
Visualisez la région.
Spécifiez un nombre Prandtl 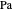 et un nombre Rayleigh
et un nombre Rayleigh 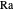 .
.
Définissez une équation visqueuse de Navier-Stokes qui est couplée à une équation de chaleur en utilisant une approximation de Boussinesq. Utilisez les paramètres de matériau qui sont spécifiés.
Définissez des conditions aux limites de non-glissement pour les vélocités sur toutes les parois des limites.
Définissez un point de pression de référence.
Spécifiez une différence de température entre les parois gauche et droite.
Remplacez les paramètres dans les conditions aux limites.
Définissez les conditions initiales de manière à ce que le système soit au repos.
Surveillez la progression de l'intégration temporelle et le temps total nécessaire pour résoudre l'EDP en utilisant un espacement du maillage spécifié et en interpolant les vélocités 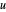 et
et 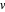 , la température
, la température 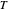 avec le second ordre et la pression
avec le second ordre et la pression 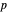 avec le premier ordre.
avec le premier ordre.
Réalisez une visualisation de la limite de la région.
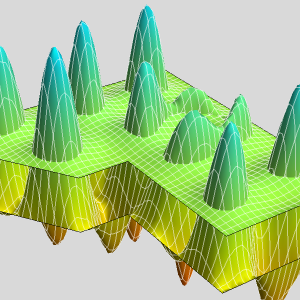
Visualisez la répartition de la pression.
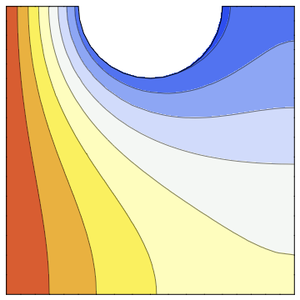
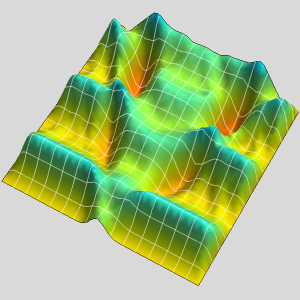
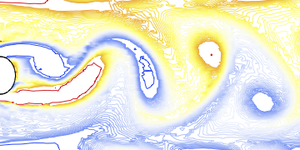
Visualisez la répartition de la température.
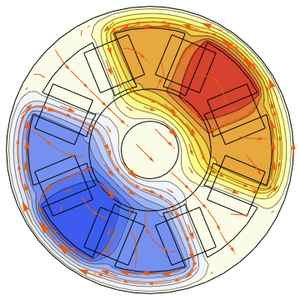
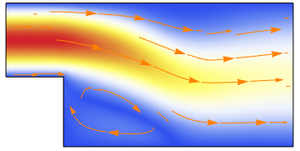
Visualisez le champ de la vélocité.
Animez le changement de température et les lignes de courant de la vélocité.
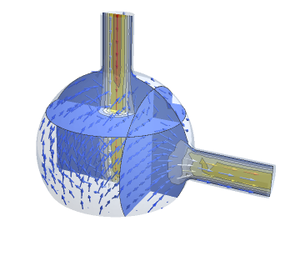
Pour les curieux, étudiez les différents champs de vélocité qui sont produits simplement en changeant les positions des découpes.