Les Éléments d'Euclide
L'un des plus anciens et des plus influents traités mathématiques de tous les temps est le traité des Éléments, une série de treize livres du mathématicien grec Euclide d'Alexandrie. Les constructions décrites dans les Éléments peuvent être représentées dans Wolfram Language en utilisant GeometricScene et visualisées avec RandomInstance.
La proposition 1 du livre I stipule qu'avec deux points 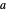 et
et 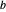 quelconques, on peut construire un triangle équilatéral avec
quelconques, on peut construire un triangle équilatéral avec 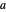 et
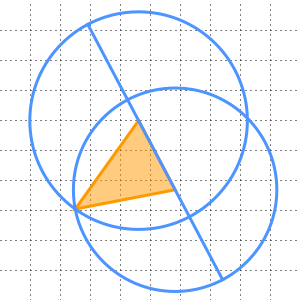
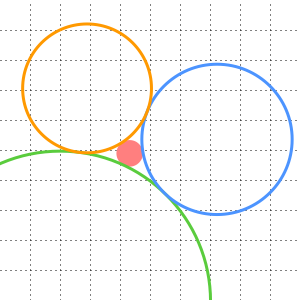
et 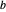 représentant deux de ses sommets. Tracez deux cercles centrés en
représentant deux de ses sommets. Tracez deux cercles centrés en 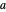 et
et 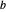 , et dont les rayons sont égaux à la distance qui les sépare. Leur point d'intersection
, et dont les rayons sont égaux à la distance qui les sépare. Leur point d'intersection 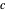 forme alors le troisième sommet d'un triangle équilatéral.
forme alors le troisième sommet d'un triangle équilatéral.
La proposition 22 du livre I généralise la proposition 1 en déclarant que pour toute grandeur positive 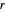 ,
, 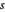 et
et 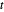 , de sorte que
, de sorte que 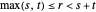 , il existe un triangle ayant des côtés de longueurs
, il existe un triangle ayant des côtés de longueurs 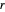 ,
, 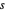 et
et 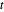 .
.
Sélectionnez au hasard les quantités positives 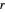 ,
, 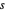 et
et 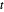 , de sorte que
, de sorte que 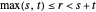 .
.
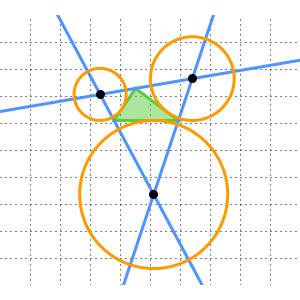
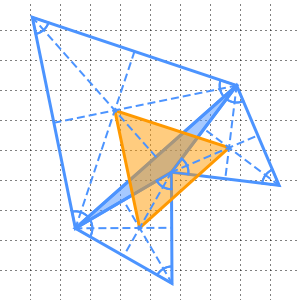
La construction se déroule comme suit : Tracez une droite passant par les points 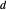 ,
, 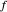 ,
, 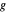 et
et 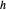 dans l'ordre, avec
dans l'ordre, avec 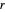 correspondant à la distance entre
correspondant à la distance entre 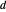 et
et 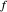 ,
, 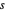 correspondant à la distance entre
correspondant à la distance entre 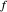 et
et 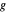 ,
, 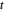 correspondant à la distance entre
correspondant à la distance entre 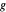 et
et 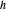 . Tracez le cercle centré en
. Tracez le cercle centré en 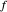 passant par
passant par 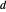 , ainsi que le cercle centré en
, ainsi que le cercle centré en 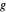 passant par
passant par 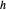 . Si
. Si 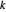 correspond à l'un des points d'intersection de ces cercles, alors
correspond à l'un des points d'intersection de ces cercles, alors 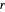 correspond à la distance entre
correspond à la distance entre 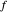 et
et 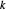 ,
, 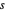 correspond à la distance entre
correspond à la distance entre 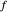 et
et 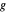 , et
, et 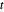 correspond à la distance entre
correspond à la distance entre 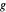 et
et 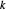 . Par conséquent, les points
. Par conséquent, les points 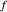 ,
, 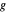 et
et 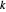 forment un triangle.
forment un triangle.