Le théorème de Viviani
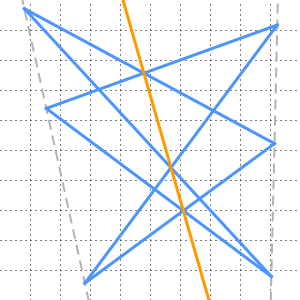
Le théorème de Viviani indique que dans un triangle équilatéral, la somme des distances de tout point intérieur aux trois côtés est égale à la hauteur du triangle. Utilisez RandomInstance pour créer une preuve visuelle du théorème de Viviani.
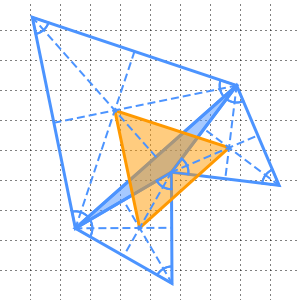
Soit 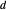 un point à l'intérieur d'un triangle équilatéral. Représentez les distances du point
un point à l'intérieur d'un triangle équilatéral. Représentez les distances du point 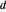 des côtés du triangle correspondant aux hauteurs des triangles équilatéraux ayant
des côtés du triangle correspondant aux hauteurs des triangles équilatéraux ayant 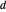 comme sommet.
comme sommet.
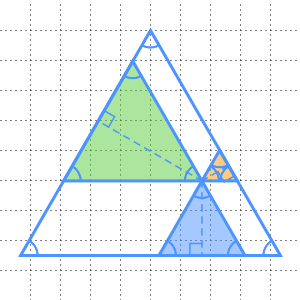
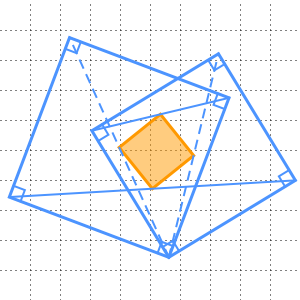
Extrayez les hauteurs des trois plus petits triangles et remarquez qu'elles correspondent en fait à la hauteur du grand triangle.
Pour comprendre ce phénomène, faites d'abord pivoter le triangle équilatéral supérieur droit, autour de son centre, à 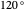 dans le sens contraire des aiguilles d'une montre, de sorte que sa hauteur soit maintenant mesurée depuis son sommet au point
dans le sens contraire des aiguilles d'une montre, de sorte que sa hauteur soit maintenant mesurée depuis son sommet au point 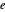 .
.
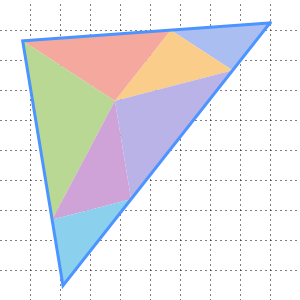
Faites pivoter le triangle équilatéral avec les sommets 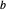 ,
, 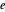 et
et 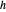 autour de son centre à
autour de son centre à 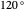 dans le sens contraire des aiguilles d'une montre.
dans le sens contraire des aiguilles d'une montre.
Maintenant, il est clair que la hauteur du grand triangle est égale à la somme des hauteurs des petits triangles.