ピタゴラス(Pythagoras)の定理
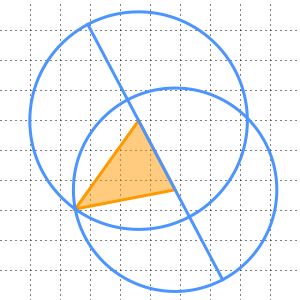
RandomInstanceは幾何学定理の可視化表現を作成するために使うことができる.直角三角形の2辺が 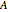 と
と 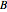 で斜辺が
で斜辺が 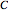 のとき
のとき 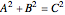 が成り立つというピタゴラスの定理は,ユークリッド幾何学の基本定理である.
が成り立つというピタゴラスの定理は,ユークリッド幾何学の基本定理である.
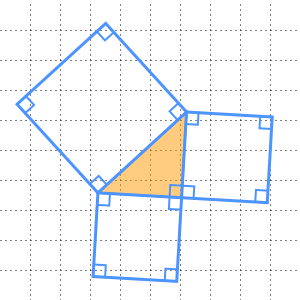
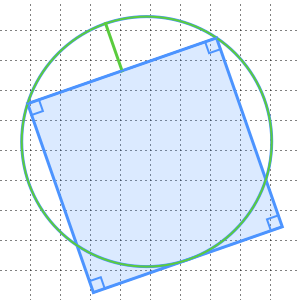
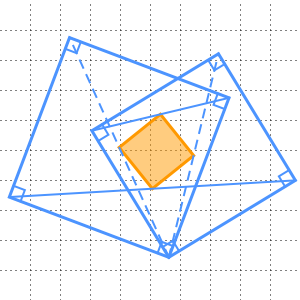
直角三角形の各辺に基づいた正方形の面積で,ピタゴラスの定理を可視化する.
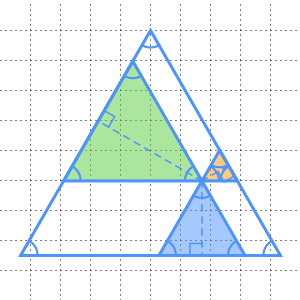
内側の正方形の各頂点が,外側の正方形の1辺を長さ 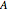 と
と 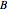 の2本の線分に分割するように,1辺の長さが
の2本の線分に分割するように,1辺の長さが 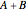 の正方形の中に一辺の長さが
の正方形の中に一辺の長さが 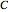 の正方形を内接させることでうまく証明できる.
の正方形を内接させることでうまく証明できる.
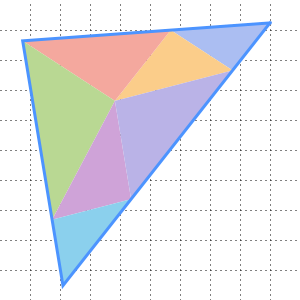
大きい方の正方形の面積は2通りの方法で計算できる.
外側の正方形の面積は1辺の長さ 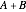 の二乗の
の二乗の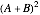 であり,
であり,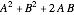 となる.
となる.
また,内側の正方形の面積は 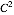 で,4つの三角形の面積はそれぞれ
で,4つの三角形の面積はそれぞれ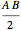 なので,大きい正方形の面積は
なので,大きい正方形の面積は 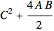 ,つまり
,つまり 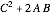 である.
である.
ゆえに 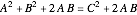 ,つまり
,つまり 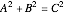 となる.
となる.