Advantage of Robust Location Measures for Heavy-Tailed Distributions
Some distributions, like Pareto or Cauchy, have a relatively high probability for "rare" events to occur. When data follows such a heavy-tail distribution, the non-robust measures of location, such as sample mean, perform poorly. In such cases, robust measures of location like the median or the biweight location are more appropriate.
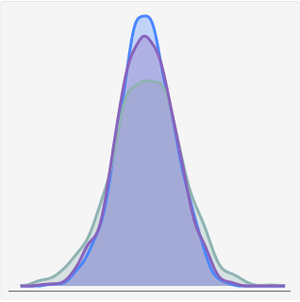
Compare the PDF of the Cauchy distribution with the PDF of the corresponding NormalDistribution, which does not have "fat" tails.
One of the characteristics of a "fat" tail distribution is that some moments, for example mean, may not be defined. As a consequence, the sample mean will be unreliable.
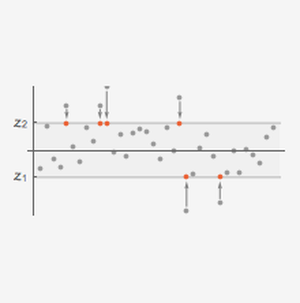
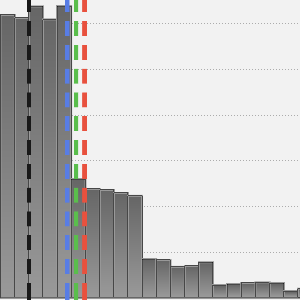
Look at the performance of location measures of data simulated from a Cauchy distribution.
Compute the central location with mean (non-robust), median (robust) and biweight location (robust).
Robust location statistics are "on average" closer to the central location of the heavy-tailed distribution.
For normally distributed data, the biweight location is close to the mean.