Vorteile von robusten Schätzverfahren bei Heavy-tailed-Verteilungen
Einige Verteilungen, wie die Pareto- oder Cauchy-Verteilung, haben eine relativ hohe Wahrscheinlichkeit, dass "seltene" Ereignisse auftreten. Wenn eine Stichprobe endlastig verteilt ist, eignen sich robuste Schätzverfahren wie das biweight-Verfahren oder die Berechnung des Medians besser als die Berechnung des arithmetischen Mittels.
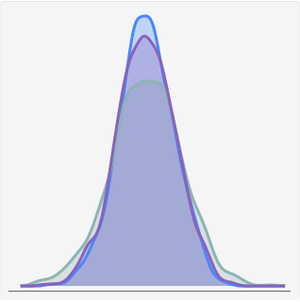
Vergleichen Sie Wahrscheinlichkeitsdichtefunktion der Cauchy-Verteilung mit der Wahrscheinlichkeitsdichtefunktion der entsprechenden NormalDistribution, die keine "schweren" Ränder hat.
Eine der Eigenschaften einer "schweren" Randverteilung ist, dass manche Momente wie das Mittel unter Umständen nicht definiert sind. Daher ist das arithmetische Mittel ein unzuverlässiger Wert.
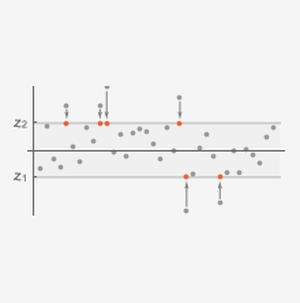
Betrachten Sie die Leistung von Lagemaßen von Daten, die aus einer Cauchy-Verteilung simuliert wurden.
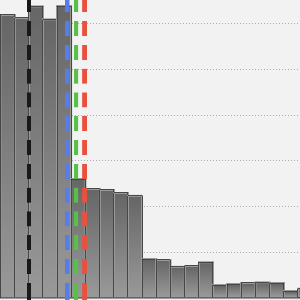
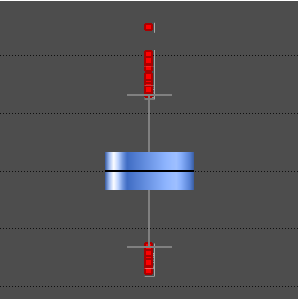
Berechnen Sie das Zentrum der Verteilung mithilfe des Mittelwerts (kein robustes Verfahren), des Medians (robustes Verfahren) und des Biweight-Verfahrens (robustes Verfahren).
Robuste statistische Schätzungsverfahren sind "im Durchschnitt" näher am Zentrum der Heavy-tailed-Verteilung dran.
Bei normalverteilten Daten liegt der Biweight-Punkt nahe dem Mittelwert.