裾の重い分布におけるロバストな位置測定値の利点
パレート分布やコーシー分布等のように,「まれな」イベントが起る確率が比較的高い分布がある.データがそのような裾の重い分布に従う場合には,単純平均等のロバストではない位置測定値はうまく機能しない.そのような場合には,中央値やbiweightの位置等のロバストな位置測定値がより適切である.
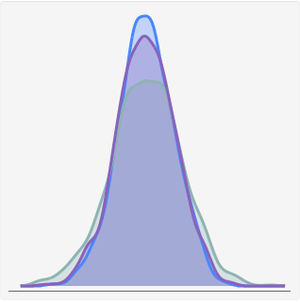
コーシー分布の確率密度関数を,対応するNormalDistributionの確率密度関数(「太い」裾を持たない)と比べる.
完全なWolfram言語入力を表示する
「太い」裾を持つ分布の特徴の一つに,例えば平均のようなモーメントは定義されない場合があるということがある.その結果,単純平均は信頼できない.
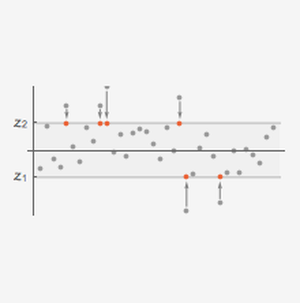
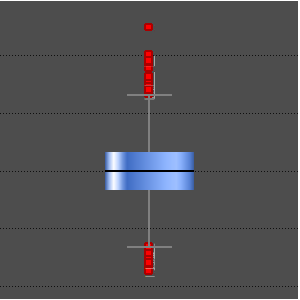
コーシー分布からシミュレーションが行われたデータの位置測定値の性能を見る.
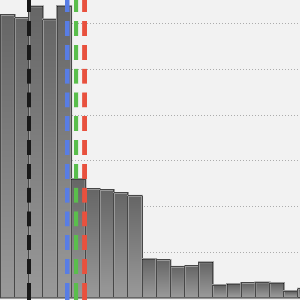
平均(ロバストではない),中央値(ロバストである),biweightの位置(ロバストである)で中心位置を計算する.
ロバストな位置統計値は,「平均して」裾の重い分布の中心位置により近いものとなる.
完全なWolfram言語入力を表示する
正規分布のデータについては,biweightの位置が平均に近い.